Hostname: page-component-cd9895bd7-fscjk Total loading time: 0 Render date: 2024-12-26T12:13:18.787Z Has data issue: false hasContentIssue false
  • English
  • Français

Simultaneous Diophantine Approximation

Published online by Cambridge University Press:  20 November 2018

Gordon Raisbeck
Gordon Raisbeck*
Affiliation:
Bell Telephone Laboratories, Murray Hill, N.J.
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Summary of results. The principal result of this paper is as follows: given any set of real numbers z1, z2, & , zn and an integer t we can find an integer 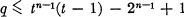and a set of integers p1, p2 & , pn such that

(0.11).

Also, if n = 2, we can, given t, produce numbers z1 and z2 such that

(0.12)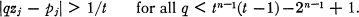

This supersedes the results of Nils Pipping (Acta Aboensis, vol. 13, no. 9, 1942) that there is a q satisfying (0.11) such that , and also the classical result of Dirichlet that there is such a q less than tn.

Type
Research Article
Information
Canadian Journal of Mathematics , Volume 2 , 1950 , pp. 283 - 288
Copyright
Copyright © Canadian Mathematical Society 1950

References

1 Here, exceptionally, t need not be an integer.