No CrossRef data available.
Published online by Cambridge University Press: 20 November 2018
Two spaces of analytic functions are considered, each comprised of functions analytic on the open disk NR(0) of radius R (0 < R < +∞ ) centred at the origin. The first space 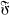 consists of all analytic functions on NR(0) topologized according to the metric of uniform convergence on compact sets. As the second space we allow any Fréchet space
consists of all analytic functions on NR(0) topologized according to the metric of uniform convergence on compact sets. As the second space we allow any Fréchet space 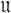 of analytic functions on NR(0) for which the topology is stronger than that induced by
of analytic functions on NR(0) for which the topology is stronger than that induced by 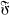 . Our objective is then to present a scheme for constructing simultaneous automorphisms on
. Our objective is then to present a scheme for constructing simultaneous automorphisms on 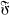 and
and 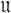 .
.