Hostname: page-component-cd9895bd7-mkpzs Total loading time: 0 Render date: 2024-12-26T19:37:07.035Z Has data issue: false hasContentIssue false
  • English
  • Français

Simple Quotients of Euclidean Lie Algebras

Published online by Cambridge University Press:  20 November 2018

Robert V. Moody
Robert V. Moody*
Affiliation:
University of Saskatchewan, Saskatoon, Saskatchewan
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

In [2], we considered a class of Lie algebras generalizing the classical simple Lie algebras. Using a field Φ of characteristic zero and a square matrix (Aij) of integers with the properties (1) Aii = 2, (2) Aij ≦ 0 if i ≠ j, (3) Aij = 0 if and only if Ajt = 0, and (4) 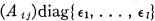is symmetric for some appropriate non-zero rational a Lie algebra E = E((Aij)) over Φ can be constructed, together with the usual accoutrements: a root system, invariant bilinear form, and Weyl group.

For indecomposable (A ij), E is simple except when (Aij) is singular and removal of any row and corresponding column of (Aij) leaves a Cartan matrix. The non-simple Es, Euclidean Lie algebras, were our object of study in [3] as well as in the present paper. They are infinite-dimensional, have ascending chain condition on ideals, and proper ideals are of finite codimension.

Type
Research Article
Information
Canadian Journal of Mathematics , Volume 22 , Issue 4 , 01 August 1970 , pp. 839 - 846
Copyright
Copyright © Canadian Mathematical Society 1970

References

1. Jacobson, N., Lie algebras (Interscience, New York, 1962).Google Scholar
2. Moody, R., A new class of Lie algebras, J. Algebra 10 (1968), 211–230.Google Scholar
3. Moody, R., Euclidean Lie algebras, Can. J. Math. 21 (1969), 1432–1454.Google Scholar
4. Serre, J.-P., Algèbres de Lie semi-simples complexes (Benjamin, New York, 1966).Google Scholar
5. Steinberg, R., Variations on a theme of Chevalley, Pacific J. Math. 9 (1959), 875–891.Google Scholar
6. Steinberg, R., Lectures on Chevalley groups, Yale University Lecture Notes, New Haven, Connecticut, 1967.Google Scholar