Hostname: page-component-586b7cd67f-2brh9 Total loading time: 0 Render date: 2024-11-20T14:42:41.546Z Has data issue: false hasContentIssue false
  • English
  • Français

Simple Algebras that Generalize the Jordan Algebra M38

Published online by Cambridge University Press:  20 November 2018

Arthur A. Sagle
Arthur A. Sagle*
Affiliation:
University of California, Los Angeles
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

In this paper we discuss a generalization of the split exceptional Jordan algebra M38(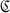) of the 3 X 3 hermitian matrices with elements in the split Cayley-Dickson algebra 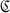(1). The generalization consists of replacing 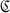by the non-commutative Jordan algebra 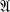≡ 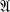(A, ƒ, s, t) discussed in (2; 3) and forming the set of 3 X 3 hermitian matrices M3m(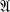) ≡ M with elements in the m-dimensional algebra 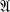. With the usual definition of multiplication X · Y = ½(XY + YX), M becomes a commutative algebra and we have the following theorem, which shows how the structure of M is reflected by that of .

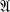Type
Research Article
Information
Canadian Journal of Mathematics , Volume 18 , 1966 , pp. 282 - 290
Copyright
Copyright © Canadian Mathematical Society 1966

References

1. Paige, L. J., Jordan algebras, Studies in Modern Algebra, vol. 2 (Amer. Math. Soc, 1963).Google Scholar
2. Paige, L. J., A note on noncommutative Jordan algebras, Portugal. Math., 16 (1957), 15–18.Google Scholar
3. Sagle, A., On anti-commutative algebras with an invariant form, Can. J. Math., 16 (1964), 370–378.Google Scholar
4. van der Waerden, B. L., Modern algebra, vol. II (New York, 1950).Google Scholar