Published online by Cambridge University Press: 20 November 2018
We extend to the setting of polynomials over a finite field certain estimates for short Kloosterman sums originally due to Karatsuba. Our estimates are then used to establish some uniformity of distribution results in the ring 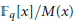 ${{\mathbb{F}}_{q}}\left[ x \right]\,/\,M\left( x \right)$ for collections of polynomials either of the form
${{\mathbb{F}}_{q}}\left[ x \right]\,/\,M\left( x \right)$ for collections of polynomials either of the form 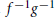 ${{f}^{-1}}{{g}^{-1}}$ or of the form
${{f}^{-1}}{{g}^{-1}}$ or of the form 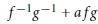 ${{f}^{-1}}{{g}^{-1}}\,+\,afg$, where
${{f}^{-1}}{{g}^{-1}}\,+\,afg$, where 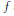 $f$ and
$f$ and 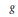 $g$ are polynomials coprime to
$g$ are polynomials coprime to 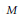 $M$ and of very small degree relative to
$M$ and of very small degree relative to 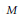 $M$, and
$M$, and 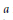 $a$ is an arbitrary polynomial. We also give estimates for short Kloosterman sums where the summation runs over products of two irreducible polynomials of small degree. It is likely that this result can be used to give an improvement of the Brun-Titchmarsh theorem for polynomials over finite fields.
$a$ is an arbitrary polynomial. We also give estimates for short Kloosterman sums where the summation runs over products of two irreducible polynomials of small degree. It is likely that this result can be used to give an improvement of the Brun-Titchmarsh theorem for polynomials over finite fields.