Hostname: page-component-cd9895bd7-fscjk Total loading time: 0 Render date: 2024-12-26T00:48:04.116Z Has data issue: false hasContentIssue false
  • English
  • Français

Sharpness in Young's Inequalityfor Convolution Products

Published online by Cambridge University Press:  20 November 2018

Ole A. Nielsen
Ole A. Nielsen*
Affiliation:
Queen's University Kingston, OntarioK7L 3N6
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Suppose that Gis a locally compact group with modular function Δ and that p, q, r are three numbers in the interval (l,∞) satisfying 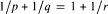. If cp,q(G) is the smallest constant c such that 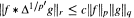for all functions f, g ∈ Cc(G) (here the convolution product is with respect to left Haar measure and 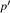is the exponent which is conjugate to p) then Young's inequality asserts that cp,q(G) ≤ 1. This paper contains three results about these constants. Firstly, if G contains a compact open subgroup then cp,q(G) = 1 and, as an extension of an earlier result of J. J. F. Fournier, it is shown that there is a constant cp,q < 1 such that if G does not contain a compact open subgroup then c<(G) ≤ c≤. Secondly, Beckner's calculation of 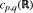is used to obtain the value of cp,q(G) for all simply-connected solvable Lie groups and all nilpotent Lie groups. And thirdly, it is shown that for a nilpotent Lie group the set 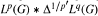is not contained in the union of the spaces Ls(G), .

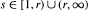Keywords

22E2522D0543A15
Type
Research Article
Information
Canadian Journal of Mathematics , Volume 46 , Issue 6 , 01 December 1994 , pp. 1287 - 1298
Copyright
Copyright © Canadian Mathematical Society 1994

References

1. Beckner, William, Inequalities in Fournier analysis, Ann. of Math. 102(1975), 159–182.Google Scholar
2. Jan Brascamp, Herm and Lieb, Elliott H., Best constants in Young's inequality, its converse, and its generalization to more than three functions, Adv. Math. 20(1976), 151–173.Google Scholar
3. Cowling, M., The Kunze-Stein phenomenon, Ann. of Math. 107(1978), 209–234.Google Scholar
4. Fournier, J. J. F., Local complements to the Hausdorff-Young theorem, Michigan Math. J. 20(1973), 263–276.Google Scholar
5. Fournier, J. J. F., Sharpness in Young-s inequality for convolution, Pacific J. Math. 72(1977), 383–397.Google Scholar
6. Hewitt, E. and Ross, K. A., Abstract Harmonic Analysis I, second edition, Springer-Verlag, Berlin, Heidelberg, New York, 1979.Google Scholar
7. Klein, Abel and Russo, Bernard, Sharp inequalities for Weyl operators and Heisenberg groups, Math. Ann. 235(1978), 175–194.Google Scholar
8. Quek, T. S. and Yap, Leonard Y. H., Sharpness of Young s inequality for convolution, Math. Scand. 53(1983), 221–237.Google Scholar
9. Saeki, Sadahiro, The LP-conjecture and Young's inequality, Illinois J. Math. 34(1990), 614–627.Google Scholar
10. Stein, Elias M., Interpolation of linear operators, Trans. Amer. Math. Soc. 83(1956), 482–492.Google Scholar
11. Varadarajan, V. S., Lie Groups, Lie Algebras, and their Representations, Prentice-Hall, Eaglewood Cliffs, 1974.Google Scholar
12. Zelazko, W., A note on Lp algebras, Colloq. Math. 10(1963), 53–56.Google Scholar