Hostname: page-component-586b7cd67f-vdxz6 Total loading time: 0 Render date: 2024-11-26T05:19:38.207Z Has data issue: false hasContentIssue false
  • English
  • Français

Shape Equivalences of Whitney Continua of Curves

Published online by Cambridge University Press:  20 November 2018

Hisao Kato
Hisao Kato*
Affiliation:
Hiroshima University, Hiroshima, Japan
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

By a compactum, we mean a compact metric space. A continuum is a connected compactum. A curve is a 1-dimensional continuum. Let X be a continuum and let C(X) be the hyperspace of (nonempty) subcontinua of X, C(X) is metrized with the Hausdorff metric (e.g., see [12] or [18]). One of the most convenient tools in order to study the structure of C(X) is a monotone map ω:C(X) → [0, ω(X)] defined by H. Whitney [25]. A map ω:C(X) → [0, ω(X)] is said to be a Whitney map for C(X) provided that

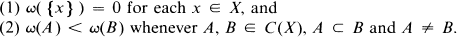
The continua {ω−1} (0 < t < ω(X)) are called the Whitney continua of X. We may think of the map ω as measuring the size of a continuum. Note that ω−1(0) is homeomorphic to X and ω−1(ω(X)) = {X}. Naturally, we are interested in the structures of ω−1(t)(0 < t < ω(X)). In [14], J. Krasinkiewicz proved that if X is a circle-like continuum and ω is any Whitney map for C(X), then for any 0 < t < ω(X)ω−1(t) is shape equivalent to X, i.e., Sh ω−1(t) = Sh X (e.g., see [1] or [17]). In [8], we proved the following: If one of the conditions (i) and (ii) is satisfied, then the shape morphism

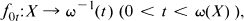
which is defined in [7] and [8], is a shape equivalence.

Type
Research Article
Information
Canadian Journal of Mathematics , Volume 40 , Issue 1 , 01 February 1988 , pp. 217 - 227
Copyright
Copyright © Canadian Mathematical Society 1988

References

1. Borsuk, K., Theory of shape, Monografie Matematyczne. 59 (Polish Scientific Publishers, Warszawa, 1975).Google Scholar
2. Case, J. H. and Chamberlin, R. E., Characterizations of tree-like continua, Pacific J. Math.. 76(1959), 73–84.Google Scholar
3. Čerin, Z. T., Homotopy properties of locally compact space at infinity — calmness and smoothness, Pacific J. Math.. 79 (1978), 69–91.Google Scholar
4. Čerin, Z. T. and Sostak, A. P., Some remarks on Borsuk's fundamental metric, Topology. I (North-Holland, New York, 1980), 233–252.Google Scholar
5. Goodykoontz, J. T. Jr. and Nadler, S. B. Jr., Whitney levels in hyperspaces of certain Peano continua, Trans. Amer. Math. Soc.. 274 (1982), 671–694.Google Scholar
6. Kato, H., Concerning hyperspaces of certain Peano continua and strong regularity of Whitney maps, Pacific J. Math.. 119 (1985), 159–167.Google Scholar
7. Kato, H., Shape properties of Whitney maps for hyperspaces, Trans. Amer. Math. Sot.. 297 (1986), 529–546.Google Scholar
8. Kato, H., Whitney continua of curves. Trans. Amer. Math. Soc, to appear.CrossRefGoogle Scholar
9. Kato, H., Whitney continua of graphs admit all homotopy types of compact connected ANRs, Fund. Math., to appear.CrossRefGoogle Scholar
10. Kato, H., Various types of Whitney maps on n-dimensional compact connected polyhedra (n ≧ 2), Topology and its Application. 97 (1986), 748–750.Google Scholar
11. Kato, H., Movability and homotopy, homology pro-groups of Whitney continua, J. Math. Soc. Japan. 39 (1987), 435–446.Google Scholar
12. Kelley, J. L., Hyperspaces of a continuum, Trans. Amer. Math. Soc.. 52 (1942), 22–36.Google Scholar
13. Krasinkiewicz, J., On the hyperspaces of snake-like and circle-like continua, Fund. Math.. 83 (1974), 155–164.Google Scholar
14. Krasinkiewicz, J., Shape properties of hyperspaces, Fund. Math.. 101 (1978), 79–91.Google Scholar
15. Krasinkiewicz, J. and Nadler, S. B. Jr, Whitney properties, Fund. Math.. 98 (1978), 165–180.Google Scholar
16. Lynch, M., Whitney levels in C(X) are absolute retracts, Proc. Amer. Math. Soc.. 97 (1986), 748–750.Google Scholar
17. Mardesic, S. and Segal, J., Shape theory (North-Holland Mathematical Library, 1982).Google Scholar
18. Nadler, S. B. Jr., Hyperspaces of sets, Pure and Appl. Math.. 49 (Dekker, New York, 1978).Google Scholar
19. Segal, J., Hyperspaces of the inverse limit space, Proc. Amer. Math. Soc.. 10 (1959), 706–709.Google Scholar
20. Rogersy, J. T. Jr., Applications of Vietoris-Begle theorem for multi-valued maps to the cohomology of hyperspaces, Michigan Math. J.. 22 (1975), 315–319.Google Scholar
21. Rogersy, J. T. Jr., The cone —hyperspace property, Can. J. Math.. 24 (1972), 279–285.Google Scholar
22. Rogersy, J. T. Jr., Whitney continua in the hyperspace C(X), Pacific J. Math.. 58 (1975), 569–584.Google Scholar
23. Spanier, E., Algebraic topology (McGraw-Hill, New York, 1966).Google Scholar
24. Ward, L. E. Jr., Extending Whitney maps, Pacific J. Math.. 93 (1981), 465–469.Google Scholar
25. Whitney, H., Regular families of curves I, Proc. Nat. Acad. Sci. U.S.A.. 18 (1932), 275–278.Google Scholar