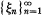Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Raimi, Ralph A.
1963.
Convergence, density, and 𝜏-density of bounded sequences.
Proceedings of the American Mathematical Society,
Vol. 14,
Issue. 5,
p.
708.
Sucheston, Louis
1964.
On existence of finite invariant measures.
Mathematische Zeitschrift,
Vol. 86,
Issue. 4,
p.
327.
Hill, J. D.
and
Sledd, W. T.
1964.
Summability- (Z, p) and Sequences of Periodic Type.
Canadian Journal of Mathematics,
Vol. 16,
Issue. ,
p.
741.
Hill, J. D.
1965.
Almost-convergent double sequences.
Tohoku Mathematical Journal,
Vol. 17,
Issue. 2,
Lloyd, S. P.
1966.
A mixing condition for extreme left invariant means.
Transactions of the American Mathematical Society,
Vol. 125,
Issue. 3,
p.
461.
Báron, J. G.
Hausner, Alvin
Gaines, Fergus
Hill, D. B.
Sucheston, Louis
Gabai, Hyman
Marcus, P. S.
Beardon, A. F.
and
Kleppner, Adam
1967.
Classroom Notes.
The American Mathematical Monthly,
Vol. 74,
Issue. 3,
p.
302.
Chou, Ching
1971.
On a geometric property of the set of invariant means on a group.
Proceedings of the American Mathematical Society,
Vol. 30,
Issue. 2,
p.
296.
Duran, J. Peter
1974.
Almost Convergence, Summability And Ergodicity.
Canadian Journal of Mathematics,
Vol. 26,
Issue. 02,
p.
372.
Nillsen, Rodney
1976.
Nets of extreme Banach limits.
Proceedings of the American Mathematical Society,
Vol. 55,
Issue. 2,
p.
347.
Talagrand, Michel
1979.
Géométrie des simplexes de moyennes invariantes.
Journal of Functional Analysis,
Vol. 34,
Issue. 2,
p.
304.
Das, G.
and
Mishra, S. K.
1981.
A note on a theorem of Maddox on strong almost convergence.
Mathematical Proceedings of the Cambridge Philosophical Society,
Vol. 89,
Issue. 3,
p.
393.
Balibrea, F.
and
Vera, G.
1986.
On the sublinear functional associated to a family of invariant means.
Manuscripta Mathematica,
Vol. 55,
Issue. 1,
p.
101.
Pietsch, Albrecht
1990.
Traces and Shift Invariant Functionals.
Mathematische Nachrichten,
Vol. 145,
Issue. 1,
p.
7.
van Douwen, Eric K.
1992.
Finitely additive measures on N.
Topology and its Applications,
Vol. 47,
Issue. 3,
p.
223.
Orhan, C.
and
Yardimci, Ş.
2004.
Banach and Statistical Cores of Bounded Sequences.
Czechoslovak Mathematical Journal,
Vol. 54,
Issue. 1,
p.
65.
Mercourakis, S.
and
Vassiliadis, G.
2009.
On some generalizations of Lorentz's almost convergence.
Journal of Mathematical Analysis and Applications,
Vol. 350,
Issue. 2,
p.
777.
Eisner, Tanja
Farkas, Bálint
Haase, Markus
and
Nagel, Rainer
2015.
Operator Theoretic Aspects of Ergodic Theory.
Vol. 272,
Issue. ,
p.
433.
Alekhno, Egor A.
2015.
On Banach–Mazur limits.
Indagationes Mathematicae,
Vol. 26,
Issue. 4,
p.
581.
Yurdakadim, T.
Khan, M. K.
Miller, H. I.
and
Orhan, C.
2016.
Generalized Limits and Statistical Convergence.
Mediterranean Journal of Mathematics,
Vol. 13,
Issue. 3,
p.
1135.
el Abdalaoui, E.H.
2019.
A non-singular dynamical system without maximal ergodic inequality.
Journal of Mathematical Analysis and Applications,
Vol. 469,
Issue. 2,
p.
960.