Hostname: page-component-5cf477f64f-2wr7h Total loading time: 0 Render date: 2025-04-08T00:23:29.641Z Has data issue: false hasContentIssue false
  • English
  • Français

Series of Products of Bessel Polynomials

Published online by Cambridge University Press:  20 November 2018

F. M. Ragab
F. M. Ragab*
Affiliation:
Institute for Advanced Study, U.S.A.andEin Shams University
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

The Bessel polynomials, which arise as solution of the classical wave equation in spherical co-ordinates, are defined by Krall and Frink (3) by the equation

1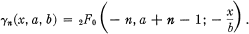

The purpose of this paper is to present some series of products of these polynomials when the two arguments are different as in the case of Legendre and Hermite polynomials. Such an explanation was given by Brafman (2), namely :

2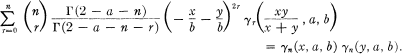

These series will be stated and proved in § 2.

Type
Research Article
Information
Canadian Journal of Mathematics , Volume 11 , 1959 , pp. 156 - 160
Copyright
Copyright © Canadian Mathematical Society 1959

References

1. Bailey, W. N., Generalized hyper geometric series, Cambr. Tracts, 32 (1935).Google Scholar
2. Brafman, Fred, A set of generating Junctions for Bessel polynomials, Froc. Amer. Math. Soc. 4 (1953), 275-7.Google Scholar
3. Krall, H. L. and Frink, O., A new class of polynomials: The Bessel polynomials, Trans. Amer. Math. Soc. 65 (1949), 100-15.Google Scholar
4. MacRoberts, T. M., Functions of a complex variable (4th ed., Glasgow, 1954).Google Scholar
5. Saalschutz, J. W., Eine Sum mations formel, Zeit. fur Math, und Phys. 35 (1890), 186-8.Google Scholar