Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Zhang, Qing
1993.
Conditional Sequence Entropy and Mild Mixing Extensions.
Canadian Journal of Mathematics,
Vol. 45,
Issue. 2,
p.
429.
Huang, Wen
Shao, Song
and
Ye, Xiangdong
2020.
Encyclopedia of Complexity and Systems Science.
p.
1.
Huang, Wen
Shao, Song
and
Ye, Xiangdong
2023.
Ergodic Theory.
p.
389.


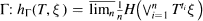 for any finite Petition ξ, and
for any finite Petition ξ, and 