Hostname: page-component-7bb8b95d7b-w7rtg Total loading time: 0 Render date: 2024-09-13T13:51:37.344Z Has data issue: false hasContentIssue false
  • English
  • Français

Semicontinuity and Multipliers of C*-Algebras

Published online by Cambridge University Press:  20 November 2018

Lawrence G. Brown
Lawrence G. Brown*
Affiliation:
Purdue University, W. Lafayette, Indiana
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

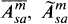In [5] C. Akemann and G. Pedersen defined four concepts of semicontinuity for elements of A**, the enveloping W*-algebra of a C*-algebra A. For three of these the associated classes of lower semicontinuous elements are , and 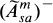(notation explained in Section 2), and we will call these the classes of strongly lsc, middle lsc, and weakly lsc elements, respectively. There are three corresponding concepts of continuity: The strongly continuous elements are the elements of A itself, the middle continuous elements are the multipliers of A, and the weakly continuous elements are the quasi-multipliers of A. It is natural to ask the following questions, each of which is three-fold.

(Q1) Is every lsc element the limit of a monotone increasing net of continuous elements?

(Q2) Is every positive lsc element the limit of an increasing net of positive continuous elements?

(Q3) If h ≧ k, where h is lsc and k is usc, does there exist a continuous x such that h ≧ x ≧ k?

Type
Research Article
Information
Canadian Journal of Mathematics , Volume 40 , Issue 4 , 01 August 1988 , pp. 865 - 988
Copyright
Copyright © Canadian Mathematical Society 1988

References

1. Akemann, C. A., The general Stone-Weierstrassproblem, J. Funct. Anal. 4 (1969), 277–294.Google Scholar
2. Akemann, C. A., Left ideal structure of C*-algebras, J. Funct. Anal. 6 (1970), 305–317.Google Scholar
3. Akemann, C. A., Approximate units and maximal abelian C*-subalgebras, Pac. J. Math. 33 (1970), 543–550.Google Scholar
4. Akemann, C. A., A Gelfand representation theory for C*-algebras, Pac. J. Math. 39 (1971), 1–11.Google Scholar
5. Akemann, C. A. and Pedersen, G. K., Complications of semicontinuity in C*-algebra theory, Duke Math. J. 40 (1973), 785–795.Google Scholar
6. Akemann, C. A. and Pedersen, G. K., Ideal perturbations of elements in C*-algebras, Math. Scand. 41 (1977), 117–139.Google Scholar
7. Akemann, C. A., Pedersen, G. K. and Tomiyama, J., Multipliers of C*-algebras, J. Funct. Anal. 75(1973), 277–301.Google Scholar
8. Akemann, C. A. and Shultz, F., Perfect C*-algebras, Memoirs A.M.S. 326 (1985).Google Scholar
9. Brown, L. G., Stable isomorphism of hereditary subalgebras of C*-algebras, Pac. J. Math. 71 (1977), 335–348.Google Scholar
10. Brown, L. G., Close hereditary C*-subalgebras and the structure of quasi-multipliers, preprpint.Google Scholar
11. Brown, L. G., Generalized crossed products of C*-algebras, in preparation.Google Scholar
12. Brown, L. G., Green, P. and Rieffel, M. A., Stable isomorphism and strong Morita equivalence of C*-algebras, Pac. J. Math. 71 (1977), 349–363.Google Scholar
13. Busby, R. C., Double centralizers and extensions of C*-algebras, Trans. Amer. Math. Soc. 132 (1968), 79–99.Google Scholar
14. Combes, F., Sur les faces d'une C*-algèbre, Bull. Sci. Math. 93 (1969), 37–62.Google Scholar
15. Combes, F., Quelques propriétés des C*-algèbres, Bull. Sci. Math. 94 (1970), 165–192.Google Scholar
16. Davis, Ch., Notions generalizing convexity for functions defined on spaces of matrices, Proc. Symp. Pure Math. 7 (Amer. Math. Soc, Providence, R.I., 1962), 187–201.Google Scholar
17. Davis, Ch., Kahan, W. M. and Weinberger, H. F., Norm-preserving dilations and their applications to optimal error bounds, SI AM J. Numer. Anal. 19 (1982), 445–469.Google Scholar
18. Dixmier, J., Les C* -algèbres et leurs représentations (Gauthier-Villars, Paris, 1964).Google Scholar
19. Dixmier, J. and A. Douady, Champs continus d'espaces hilbertiens et de C*-algèbres, Bull. Soc. Math. France 91 (1963), 227–284.Google Scholar
20. Effros, E. G., Order ideals in a C*-algebra and its dual, Duke Math. J. 30 (1963), 391–412.Google Scholar
21. Hansen, F., An operator inequality, Math. Ann. 246 (1980), 249–250.Google Scholar
22. Hansen, F. and Pedersen, G. K., Jensen's inequality for operators and Löwner's theorem, Math. Ann. 258 (1982), 229–241.Google Scholar
23. Kasparov, G. G., Hilbert C*-modules: theorems of Stinespring and Voiculescu, J. Operator Theory 4 (1980), 133–150.Google Scholar
24. Michael, E. A., Continuous selections I, Ann. Math. 63 (1956), 361–382.Google Scholar
25. Mingo, J. A. and Phillips, W. J., Equivariant triviality theorems for Hilbert C*-modules, Proc. Amer. Math. Soc. 91 (1984), 225–230.Google Scholar
26. Olesen, D. and Pedersen, G. K., Derivations of C*-algebras have semi-continuous generators, Pac. J. Math. 53 (1974), 563–572.Google Scholar
27. Parrott, S. K., On a quotient norm and the Sz.-Nagy-Foias lifting theorem, J. Funct. Anal. 30(1978), 311–328.Google Scholar
28. Pedersen, G. K., Applications of weak* semicontinuity in C*-algebra theory, Duke Math. J. 39 (1912), 431–450.Google Scholar
29. Pedersen, G. K., C*-algebras and their automorphism groups (Academic Press, London, 1979).Google Scholar
30. Pedersen, G. K., SAW*-algebras and corona C*-algebras, contributions to non-commutative topology, J. Operator Theory (to appear).Google Scholar
31. Shen, N. T., Embeddings of Hilbert bimodules, preprint.Google Scholar
32. Størmer, E., Two-sided ideals in C*-algebras, Bull. Amer. Math. Soc. 73 (1967), 254–257.Google Scholar
33. Tomita, M., Spectral theory of operator algebras, I, Math. J. Okayama Univ. 9 (1959), 63–98.Google Scholar