Hostname: page-component-cd9895bd7-hc48f Total loading time: 0 Render date: 2024-12-23T18:51:09.840Z Has data issue: false hasContentIssue false
  • English
  • Français

Semi-classical Integrability, Hyperbolic Flows and the Birkhoff Normal Form

Published online by Cambridge University Press:  20 November 2018

Michel Rouleux
Michel Rouleux*
Affiliation:
Université de Toulon et du Var and Centre de Physique Théorique, Unité Propre de Recherche 7061, CNRS Luminy, Case 907, 13288 Marseille Cedex 9, France email: [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

We prove that a Hamiltonian 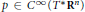$p\in {{C}^{\infty }}({{T}^{*}}{{\mathbf{R}}^{n}})$ is locally integrable near a non-degenerate critical point 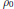${{\rho }_{0}}$ of the energy, provided that the fundamental matrix at 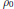${{\rho }_{0}}$ has rationally independent eigenvalues, none purely imaginary. This is done by using Birkhoff normal forms, which turn out to be convergent in the 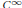${{C}^{\infty }}$ sense. We also give versions of the Lewis-Sternberg normal form near a hyperbolic fixed point of a canonical transformation. Then we investigate the complex case, showing that when 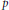$p$ is holomorphic near 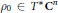${{\rho }_{0}}\in {{T}^{*}}{{\mathbf{C}}^{n}},$ then Re 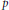$p$ becomes integrable in the complex domain for real times, while the Birkhoff series and the Birkhoff transforms may not converge, i.e.,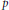$p$ may not be integrable. These normal forms also hold in the semi-classical frame.

Keywords

35S37J1070H08
Type
Research Article
Information
Canadian Journal of Mathematics , Volume 56 , Issue 5 , 01 October 2004 , pp. 1034 - 1067
Copyright
Copyright © Canadian Mathematical Society 2004

References

[AbMar] Abraham, R., Marsden, J., The foundations of mechanics. Benjamin, N.Y. Revised edition, 1978.Google Scholar
[AbRob] Abraham, R., Robbin, J. (with an Appendix by Kelley, A.), Transversal mappings and flows. Benjamin, New York, 1967.Google Scholar
[Ar] Arnold, V., Les méthodes mathématiques de la mécanique classique. Éditions Mir, Moscow, 1976.Google Scholar
[ArNo] Arnold, V., and Novikov, S., eds., Dynamical systems III-IV. Encyclopaedia of Mathematics. Springer-Verlag Berlin, 1988–1990.Google Scholar
[ArVaGo] Arnold, V., Varchenko, A., Goussein-Zadé, S., Singularités des applications différentiables I. Éditions Mir, Moscow, 1986.Google Scholar
[Au] Audin, M., Les systèmes Hamiltoniens et leur intégrabilité. Soc. Math. France 8(2001).Google Scholar
[BamGraPa] Bambusi, D., Graffi, S., Paul, Th., Normal forms and quantization formulae. Comm. Math. Phys. 207(1999) 173–195.Google Scholar
[BaLlWa] Banyaga, A., de La Llave, R., Wayne, C., Cohomology equations near hyperbolic points and geometric versions of Sternberg linearization theorem. J. Geom. Anal. 690(1996), 613–649,.Google Scholar
[BeKo1] Belitskii, G., Kopanskii, A., Sternberg theorem for equivariant Hamiltonian vector fields. Nonlinear Anal. 47(2001), 4491–4499,.Google Scholar
[BeKo2] Belitskii, G., Kopanskii, A., Sternberg-Chen theorem for equivariant Hamiltonian vector fields. In: Symmetry and perturbation theory III – SPT2001, Bambusi, D., Cadoni, M. and Gaeta, G. eds., World Scientific, River Edge, NJ, 2001.Google Scholar
[Bi] Birkhoff, G. D., Dynamical systems. Amer. Math. Soc. Colloquium Publ. 1927, revised ed. 1966.Google Scholar
[BrKo] Bronstein, I. and Kopanskii, A., Normal forms of vector fields satisfying certain geometric conditions. In: Nonlinear dynamical systems and chaos. Birkhäuser, Basel, 1996, pp. 79–101.Google Scholar
[Bru] Bruhat, F., Travaux de Sternberg. Séminaire Bourbaki 6, (1995), 179–196.Google Scholar
[Ch1] Chen, K.-T., Collected papers of K.-T. Chen, Birkhäuser Boston, Boston, MA, 2001.Google Scholar
[Ch2] Chen, K.-T., Equivalence and decomposition of vector fields about an elementary critical point. Amer. J. Math. 85(1963), 693–722 (reprinted in [Ch1]).Google Scholar
[CuB] Cushman, R., Bates, L., Global aspects of classical integrable systems. Birkhäuser-Verlag, Basel, 1997.Google Scholar
[Ec] Ecalle, J., Introduction aux fonctions analysables et preuve constructive de la conjecture de Dulac. Hermann, Paris, 1992.Google Scholar
[El] Eliasson, L. H., Normal forms for Hamiltonian systems with Poisson commuting integrals—elliptic case. Comment.Math. Helv. 65(1990), 4–35,.Google Scholar
[Fr] Franc¸oise, J. P., Propriétés de généricité des transformations canoniques. In: Geometric dynamics, Palis, J., ( ed.), Springer-Verlag, 1983, pp. 216–260.Google Scholar
[Gal] Gallavotti, G., The Elements of mechanics. Springer-Verlag, New York, 1983.Google Scholar
[GeSj] Gérard, C. and Sjöstrand, J., Semiclassical resonances generated by a closed trajectory of hyperbolic type. Comm. Math. Phys. 108(1987), 391–421, .Google Scholar
[GiDeFoGaSim] Giorgilli, A., Delsham, A., Fontich, E., Galgani, L. and Simò, C., Effective stability for a Hamiltonian system near an equilibrium point with an application to the restricted three-body problem. J. Differential Equations 77(1989), 167–198,.Google Scholar
[Gr] Graff, S., On the conservation of hyperbolic tori for Hamiltonian systems. J. Differential Equations 15(1974), 1–69,Google Scholar
[GuSc] Guillemin, V. and Schaeffer, D., On a certain class of fuchsian partial differential equations. Duke Math. J. 44(1977), 157–199,.Google Scholar
[Ha] Hartman, P., Ordinary differential equations. Wiley, New York, 1964.Google Scholar
[HeSj1] Helffer, B. and Sjöstrand, J., Multiple wells in the semi-classical limit III. Interaction through non-resonant wells. Math. Nachr. 124(1985), 263–313.Google Scholar
[HeSj2] Helffer, B. and Sjöstrand, J., Semi-classical analysis for Harper's equation III. Soc. Math. France, Mém. (N.S.) 39(1989).Google Scholar
[HiPuSh] Hirsch, M., Pugh, C. and Shub, M., Invariant manifolds. Lecture Notes in Mathematics, 583, Springer-Verlag, Berlin, 1977.Google Scholar
[IaSj] Iantchenko, A. and Sjöstrand, J., Birkhoff normal forms for Fourier integral operators II. Amer. J. Math. 124)2002), 817–850.Google Scholar
[It] Ito, H., Integrable symplectic maps and their Birkhoff normal form. Tohoku Math. J. 49(1997), 73–114.Google Scholar
[Iv] Ivrii, V., Microlocal analysis and precise spectral asymptotics. Springer-Verlag, Berlin, 1998.Google Scholar
[KaRo] Kaidi, N. and Rouleux, M., Quasi-invariant tori and semi-excited states for Schrödinger operators I. Asymptotics. Comm. Partial Differential Equations 27(2002), 1695–1750.Google Scholar
[M] Malliavin, P., Géométrie différentielle intrinsèque. Hermann, Paris, 1972.Google Scholar
[MaSo] Martinez, A. and Sordoni, V., Microlocal WKB expansions. J. Funct. Anal. 168(1999), 380–402.Google Scholar
[MeSj] Melin, A. and Sjöstrand, J., Determinants of pseudo-differential operators and complex deformations of phase space. Methods Appl. Anal. 9(2002), 177–237.Google Scholar
[Mo] Moser, J., On the generalization of a theorem of A. Lyapunoff. Comm. Pure Appl. Math. 11(1958), 257–271, .Google Scholar
[Ne] Nelson, E., Topics in dynamics I: Flows. Princeton University Press, Princeton, NJ, 1969.Google Scholar
[Ro1] Rouleux, M., Quasi-invariant tori and semi-excited states for Schrödinger operators II. Tunneling. In preparation.Google Scholar
[Ro2] Rouleux, M., Integrability of an holomorphic Hamiltonian near a hyperbolic fixed point. In preparation.Google Scholar
[Si1] Siegel, C. L., Über die Normalform analytischer Differentialgleichungen in der Nähe einer Gleichgewichtslösung. Nachr. Akad. Wiss. Göttingen (1952), 21–30.Google Scholar
[Si2] Siegel, C. L., Über die Existenz einer Normalform analytischer Differentialgleichungen in der Nähe einer Gleichgewichtslösung Math. Ann. 128(1954), 144–170.Google Scholar
[SiMo] Siegel, C. L. and Moser, J., Lectures on celestial mechanics, Springer-Verlag, Berlin, 1971.Google Scholar
[Sie] Siegmund, S., Normal forms for nonautonomous differential equations. J. Differential Equations 178(2001), 541–573.Google Scholar
[Sj1] Sjöstrand, J., Singularités analytiques microlocales. Astérisque 95(1982).Google Scholar
[Sj2] Sjöstrand, J., Analytic wavefront sets and operators with multiple characteristics. Hokkaido Math. J. 12(1983), 392–433.Google Scholar
[Sj3] Sjöstrand, J., Semi-excited states in nondegenerate potential wells. Asymptotic Anal. 6(1992), 29–43, .Google Scholar
[SjZw] Sjöstrand, J. and Zworski, M., Quantum monodromy and semiclassical trace formulae. J. Math. Pures Appl. 81(2002), 1–33.Google Scholar
[St] Sternberg, S., The structure of local diffeomorphisms III. Amer. J. Math. 81(1959), 578–604.Google Scholar
[Vi] Vittot, M., Birkhoff expansions in Hamiltonian mechanics: a simplification of the combinatorics. In: Non-linear dynamics, Turchetti, G., (ed.) World Scientific, Teaneck, NJ, 1989, pp. 276–286.Google Scholar
[Vu1] Vu Ngoc, S., Sur le spectre des systèmes complètement intégrables semi-classiques avec singularités. Ph.D. Thesis, Université de Grenoble, 1998.Google Scholar
[Vu2] Vu Ngoc, S., On semi-global invariants for focus-focus singularities. Topology 42(2003), 365–380.Google Scholar