Hostname: page-component-cd9895bd7-dzt6s Total loading time: 0 Render date: 2024-12-23T20:01:16.432Z Has data issue: false hasContentIssue false
  • English
  • Français

Rigidity and Height Bounds for Certain Post-critically Finite Endomorphisms of ℙN

Published online by Cambridge University Press:  20 November 2018

Patrick Ingram
Patrick Ingram*
Affiliation:
Colorado State University, Fort Collins, CO, USA e-mail: [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

The morphism 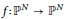$f\,:\,{{\mathbb{P}}^{N}}\,\to \,{{\mathbb{P}}^{N}}$ is called post-critically finite 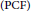$\left( \text{PCF} \right)$ if the forward image of the critical locus, under iteration of 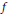$f$ , has algebraic support. In the case 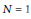$N\,=\,1$ , a result of Thurston implies that there are no algebraic families of PCF morphisms, other than a well-understood exceptional class known as the flexible Lattés maps. A related arithmetic result states that the set of PCF morphisms corresponds to a set of bounded height in the moduli space of univariate rational functions. We prove corresponding results for a certain subclass of the regular polynomial endomorphisms of 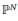${{\mathbb{P}}^{N}}$ for any 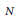$N$ .

Keywords

37P1532H5037P30post–critically finitearithmetic dynamicsheights
Type
Research Article
Information
Canadian Journal of Mathematics , Volume 68 , Issue 3 , 01 June 2016 , pp. 625 - 654
Copyright
Copyright © Canadian Mathematical Society 2016

References

[1]Baker, M. and DeMarco, L., Preperiodic points and unlikely intersections Duke Math. Journal. 159 (2011), no. 1, pp. 1–29. http://dx.doi.org/10.1215/00127094-1384773 Google Scholar
[2] Baker, M. andDeMarco, L., Special curves and postcritically-ûnite polynomials, Forum Math., Pi, 1 (2013), e3 (35 pages).http://dx.doi.org/10.1017/fmp.2013.2 Google Scholar
[3] Bedford, E. and Jonsson, M., Dynamics of regular polynomial endomorphisms of Ck, Amer. J. Math. 122 (2000), pp. 153–212. http://dx.doi.org/10.1353/ajm.2000.0001 Google Scholar
[4] Benedetto, R. L., Ingram, P., Jones, R., and Levy, A., Attracting cycles in p-adic dynamics and height bounds for post-critically finite maps. Duke Math. J. 163 no. 13 (2014), pp.2325–2356 http://dx.doi.org/10.1215/00127094-2804674 Google Scholar
[5] Benedetto, R. L., A Criterion for Potentially Good Reduction in Non-archimedean Dynamics. Acta Arith. 165 (2014), pp.251–256. http://dx.doi.org/10.4064/aa165-3-4 Google Scholar
[6] Bost, J.-B., Gillet, H., and Soulé, C., Heights of projective varieties and positive Green forms J.Amer. Math. Soc. 7 (1994),no.pp.903–1027. http://dx.doi.org/10.1090/S0894-0347-1994-1260106-X Google Scholar
[7] Call, G. S. and Silverman, J. H., Canonical heights on varieties with morphisms Compositio Math 89 (1993), pp.163–205.Google Scholar
[8] DeMarco, L., Hruska, S. L., Axiom A polynomial skew products of Cz and their postcritical sets Ergodic Theory Dynam. Systems 28 (2008) pp. 1729–1748.http://dx.doi.org/10.1017/S0143385708000047 Google Scholar
[9] Dinh, T.-C., Sur les applications de Lattés de Pk , J. Math. Pures Appl. (9) 80 (2001), no. 6, pp. 577–592.http://dx.doi.org/10.1016/S0021-7824(01)01205-3 Google Scholar
[10] Epstein, A. L., Integrality and rigidity for postcritically finite polynomials,With an appendix by Epstein and Bjorn Poonen.Bull. Lond. Math. Soc. 44(2012), no. 1, pp.39–46. http://dx.doi.org/10.1112/blms/bdr059 Google Scholar
[11] Favre, C. and Gauthier, T., Distribution of postcritically finite polynomials, arXiv:1302.0810. http://dx.doi.org/10.1007/s11856-015-1218-0 Google Scholar
[12] Fornæss, E. and Sibony, N., Critically finite rational maps on P2. The Madison Symposium on Complex Analysis (Madison, WI, 1991), pp. 245–260, volume 137 of Contemp. Math., Amer. Math. Soc., Providence, RI, 1992.Google Scholar
[13]Ingram, P., Variation of the canonical height for a family of polynomials J. Riene Ange. Math. (to appear).Google Scholar
[14] Ingram, P., A finiteness result for post–critically finite polynomials, Int. Math. Res. Not. 2012, no. 3, pp. 524–543.Google Scholar
[15] Ingram, P., Variation of the canonical height for polynomials in several variables, Int. Math. Res. Not. (to appear)doi:10.1093/imrn/rnv121 Google Scholar
[16] Jonsson, M., Some properties of z–critically ûnite holomorphic maps of P2. Ergodic Theory Dynam. Systems 18 (1998), no. 1, pp. 171–187. http://dx.doi.org/10.1017/S0143385798097521 Google Scholar
[17] M.Jonsson, , Dynamics of polynomial skew products on C2. Math. Ann. 314(1999), no.3 ,pp.403–447. http://dx.doi.org/10.1007/s002080050301 Google Scholar
[18] Jouanolou, J.-P., Le formalisme du résultant. Adv. Math. 90 (1991), no. 2, pp. 117–263.http://dx.doi.org/10.1016/0001-8708(91)90031-2 Google Scholar
[19] Koch, S., Teichmüller theory and critically unite endomorphisms. Adv. Math. 248(2013), pp. 573–617 http://dx.doi.org/10.1016/j.aim.2013.08.019 Google Scholar
[20] Levy, A., An algebraic proof of Thurston's rigidity for a polynomial (arXiv:1201.1969)Google Scholar
[21] Masser, D. and Wüstholz, G., Fields of large transcendence degree generated by values of elliptic functions Invent. Math 72 (1983), pp. 407–464.http://dx.doi.org/10.1007/BF01398396 Google Scholar
[22] Minimair, M., MR package for Maple, 2007, http://minimair.org/mr. Google Scholar
[23] Moriwaki, A., Arithmetic height functions over finitely generated fields, Invent. Math.140 (2000), no. 1, pp.101–142. z. http://dx.doi.org/10.1007/s002220050358 Google Scholar
[24] Rong, F., The Fatou set for critically finite maps. Proc. Amer. Math. Soc., 136 (2008), pp. 3621–3625. http://dx.doi.org/10.1090/S0002-9939-08-09358-1 Google Scholar
[25] Rong, F., Lattés maps on P2. J. Math. Pures Appl. (9)93 (2010), no. 6, pp. 636–650.http://dx.doi.org/10.1016/j.matpur.2009.10.002 Google Scholar
[26] Philippon, P., Sur des hauteurs alternativesI. Math. Ann 289 (1991), no. 2, pp. 255–283.Google Scholar
[27] Silverman, J. H., The Arithmetic of Dynamical Systems, volume 241 of Graduate Texts in Mathematics. Springer, 2007.http://dx.doi.org/10.1007/BF01446571 Google Scholar
[28] JSilverman, . H., Moduli Spaces and Arithmetic Dynamics, volume 30 of CRM Monograph Series. AMS, 2012.Google Scholar
[29] Silverman, J. H., An algebraic approach to certain cases of Thurston rigidity. Proc. Amer. Math. Soc.140 (2012), no.10 , pp. 3421–3434 http://dx.doi.org/10.1090/S0002-9939-2012-11171-2 Google Scholar
[30] Stein, W. A. et al., Sage Mathematics Software (Version 5.8–OSX–64 bit–10.8), The Sage Development Team, http://www.sagemath.org. Google Scholar
[31] Douady, A. and Hubbard, J., A proof of_urston's topological characterization of rational functions Acta Math. 171 (1993), pp. 263–297.http://dx.doi.org/10.1007/BF02392534 Google Scholar
[32] Uchimura, K., Generalized Chebyshev maps of C2 and their perturbations. Osaka J. Math. 46(2009), no.4, pp.995–1017.Google Scholar
[33] Ueda, T., Critical orbits of holomorphic maps on projective spaces. J. Geom. Anal. 8 (1998), Issue 4, pp. 319–334. http://dx.doi.org/10.1007/BF02921645 Google Scholar
[34] Veselov, A., Integrable mappings and Lie algebras. Dokl. Akad. Nauk SSSR 292 (1987), no.6 ,pp.1289–1291.Google Scholar
[35] Zdunik, A., Parabolic orbifolds and the dimension of the maximal measure for rational maps. Invent. Math. 99 (1990), no. h, pp.627–649 http://dx.doi.org/10.1007/BF01234434 Google Scholar
[36] Zhang, S., Small points and adelic metrics. J. Algebraic Geom. 4 (1995), no. 2, pp. 281–300.Google Scholar