Hostname: page-component-78c5997874-g7gxr Total loading time: 0 Render date: 2024-11-16T18:01:21.219Z Has data issue: false hasContentIssue false
  • English
  • Français

Right Bol Quasi-Fields

Published online by Cambridge University Press:  20 November 2018

Michael J. Kallaher
Michael J. Kallaher*
Affiliation:
The University of Manitoba, Winnipeg, Manitoba; Washington State University, Pullman, Washington
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

We shall consider quasi-fields which satisfy the multiplicative Identity

1.1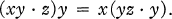

(1.1) will be called the right Bol law and a quasi-field satisfying it will be called a right Bol quasi-held. Moufang quasi-fields, i.e., those satisfying the Moufang identity

1.2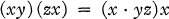

were studied in (5). Quasi-fields satisfying the left Bol identity

1.3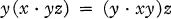

were studied by Burn (3) and the author (6). Such quasi-fields are called Bol quasi-fields.

Our investigation will parallel the investigations in (5; 6). In § 2 we derive necessary and sufficient conditions for a right Bol quasi-field to be an alternative division ring and also criteria for it to be a near-field. With this information we derive in §§ 3 and 4 new characterizations of Moufang planes similar to those in (5; 6).

Loops satisfying (1.1) have been studied by Robinson (10). He calls such loops Bol loops.

Type
Research Article
Information
Canadian Journal of Mathematics , Volume 21 , 1969 , pp. 1409 - 1420
Copyright
Copyright © Canadian Mathematical Society 1969

References

1. André, Johannes, Projektiven Ebenen iiber Fastkôrpern, Math. Z. 62 (1955), 137–160.Google Scholar
2. Bol, G., Topologische Fragen der Differentialgeometrie, 65, Gewebe und Gruppen, Math. Ann. 114 (1937), 414–431.Google Scholar
3. Burn, Robert, Bol quasi-fields and Pappus's theorem, Math. Z. 105 (1968), 351–364.Google Scholar
4. Hall, Marshall, Jr., Theory of groups (Macmillan, New York, 1959).Google Scholar
5. Kallaher, Michael J., Moufang Veblen-Wedderburn systems, Math. Z. 105 (1968), 1.Google Scholar
6. Kallaher, Michael J., Projective planes over Bol quasi-fields, Math. Z. 109 (1969), 53–65.Google Scholar
7. Klingenberg, Wilhelm, Beziehungen zwischen einigen affinen Schliessungssdtzen, Abh. Math. Sem. Univ. Hamburg 18 (1952), 120–143.Google Scholar
8. Klingenberg, Wilhelm, Beweis des Desarguesschen Satzes aus der Reidemeisterfigur und verwandte Sâtze, Abh. Math. Sem. Univ. Hamburg 19 (1955), 158–175.Google Scholar
9. Pickert, Gunter, Projektive Ebenen (Springer-Verlag, Berlin, 1955).Google Scholar
10. Robinson, D. A., Bol loops, Trans. Amer. Math. Soc. 123 (1966), 341–354.Google Scholar
11. San Soucie, R. L., Right alternative division rings of characteristic two, Proc. Amer. Math. Soc. 6 (1955), 291–296.Google Scholar
12. Skornyakov, L. A., Right-alternative fields, Izv. Akad. Nauk SSSR Ser. Mat. 15 (1951), 177–184. (Russian)Google Scholar