Hostname: page-component-586b7cd67f-t8hqh Total loading time: 0 Render date: 2024-11-26T09:50:48.865Z Has data issue: false hasContentIssue false
  • English
  • Français

Riesz Decompositions

Published online by Cambridge University Press:  20 November 2018

Alexander Nagel  and
Walter Rudin
Alexander Nagel
Affiliation:
University of Wisconsin, Madison, Wisconsin
Walter Rudin
Affiliation:
University of Wisconsin, Madison, Wisconsin
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

All functions mentioned in this paper will be real-valued. If f1, f2, g are nonnegative functions on a set S that satisfy g ≦ f1 + f2, the Riesz decomposition problem associated with these data is to find functions gi on S such that

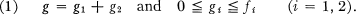
The formula

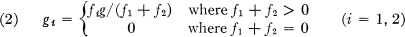
always furnishes a solution. The problem becomes more interesting if one asks under what conditions one can find solutions that are, roughly speaking, as smooth as the data.

Type
Research Article
Information
Canadian Journal of Mathematics , Volume 26 , Issue 3 , June 1974 , pp. 753 - 760
Copyright
Copyright © Canadian Mathematical Society 1974

References

1. Buck, R. C., The Riesz property of a partially ordered linear space, Notices Amer. Math. Soc. 5 (1958), p. 31.Google Scholar
2. Dieudonné, Jean, Sur un théorème de Glaeser, J. Analyse Math. 23 (1970), 85–88.Google Scholar
3. Namioka, Isaac, Partially ordered linear topological spaces, Mem. Amer. Math. Soc. 24 (1957).Google Scholar
4. Rudin, Walter, Real and complex analysis (McGraw-Hill, New York, 1966).Google Scholar
5. Schaefer, Helmut, Halbgeordnete lokalkonvexe Vektorräume, Math. Ann. 141 (1960), 113–142.Google Scholar