Hostname: page-component-586b7cd67f-tf8b9 Total loading time: 0 Render date: 2024-11-20T06:58:33.540Z Has data issue: false hasContentIssue false
  • English
  • Français

Rich Proximities and Compactifications

Published online by Cambridge University Press:  20 November 2018

Stephan C. Carlson
Stephan C. Carlson*
Affiliation:
University of North Dakota, Grand Forks, North Dakota
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Each Hausdorff compactification of a given Tychonoff space is the Smirnov compactification associated with a compatible proximity on the space. Also each realcompactification of a given Tychonoff space is the underlying topological space of the completion of a compatible uniformity on the space. But if T is a realcompactification of a Tychonoff space X which is contained in a particular compactification Z of X, then it is not always possible to find a compatible uniformity 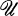on X such that T is the underlying topological space of the completion of (X, 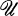) and 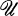induces the proximity on X associated with Z. We shall call a Hausdorff compactification Z of a Tychonoff space X a rich compactification of X (and the associated proximity on X a rich proximity) if every realcompactification of X contained in Z can be obtained as the underlying topological space of the completion of a compatible uniformity on X which induces the proximity on X associated with Z.

Type
Research Article
Information
Canadian Journal of Mathematics , Volume 34 , Issue 2 , 01 April 1982 , pp. 319 - 348
Copyright
Copyright © Canadian Mathematical Society 1981

References

1. Bachman, G., Beckenstein, E., Narici, L. and Warner, S., Rings of continuous functions with values in a topological field, Trans. Amer. Math. Soc. 204 (1975), 91–112.Google Scholar
2. Banaschewski, B., Ûber nulldimensionale Rdume, Math. Nachr. 13 (1955), 129–140.Google Scholar
3. Banaschewski, B., A remark on extensions of Hausdorff spaces, General Topology and its Applications 4 (1974), 283–284.Google Scholar
4. Carlson, S. C., Rich proximities on Tychonoff spaces, Ph.D. dissertation, University of Kansas, Lawrence, Kansas (1978).Google Scholar
5. Chew, K. P., Shirota's theorem for N-compact spaces, Kyungpook Math. J. 12 (1972), 153–157.Google Scholar
6. Dugundji, J., Topology (Allyn and Bacon, Boston, Mass., 1966).Google Scholar
7. Engelking, R. and Mrôwka, S., On E-compact spaces, Bull. Acad. Polon. Sci. Ser. Sci. Math. Astronom. Phys. 6 (1958), 429–435.Google Scholar
8. Ganter, T., Extensions of uniform structures, Fund. Math. 66 (1970), 263–281.Google Scholar
9. Gillman, L. and Jerison, M., Rings of continuous functions (D. Van Nostrand Co., Princeton, New Jersey, 1960).Google Scholar
10. Herrlich, H. and VanderSlot, J., Properties which are closely related to compactness, Indag. Math. 29 (1967), 524–529.Google Scholar
11. Marin, F., A note on E-compact spaces, Fund. Math. 76 (1972), Fasc. 3, 195–206.Google Scholar
12. Mrowka, S., Recent results on E-compact spaces, TOPO 72-General Topology and its Applications, Second Pittsburgh International Conference (1972), 298–301.Google Scholar
13. Nyikos, P., Not every 0-dimensional realcompact space is N-compact, Bull. Amer. Math. Soc. 77 (1971), 392–396.Google Scholar
14. Piacun, N. and Su, L. P., Woilman compactifications on E-completely regular spaces, Pacific J. Math. 45 (1973), 321–326.Google Scholar
15. Su, L. P., Wallman-type compactifications on 0-dimensional spaces, Proc. Amer. Math. Soc. 43 (1974), 455–460.Google Scholar
16. Thron, W. J., Topological structures (Holt, Rinehart and Winston, New York, 1966).Google Scholar
17. Weir, M., Hewitt-Nachbin spaces, Notes de Matemâtica 57 (North-Holland Publishing Co., 1975).Google Scholar
18. Willard, S., General topology (Addison-Wesley Publishing Co., Reading, Mass., 1970).Google Scholar
19. Woods, R. G., Topological extension properties, Trans. Amer. Math. Soc. 210 (1975), 365–385.Google Scholar