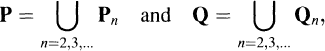Hostname: page-component-586b7cd67f-t7fkt Total loading time: 0 Render date: 2024-11-28T02:40:18.924Z Has data issue: false hasContentIssue false
  • English
  • Français

Rewritable Products In Fc-By-Finite Groups

Published online by Cambridge University Press:  20 November 2018

Russell D. Blyth  and
Akbar H. Rhemtulla
Russell D. Blyth
Affiliation:
Saint Louis University, St. Louis, Missouri
Akbar H. Rhemtulla
Affiliation:
University of Alberta, Edmonton, Alberta
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let n be an integer greater than 1. The group G has the property Q„, or is n-rewritable, if for each «-element subset ﹛x1 x 2… ,x n﹜ of G, there exist permutations 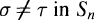such that 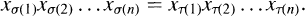If one of ᓂ,τ can always be chosen to be the identity, then G has Pn, or is totally n-rewritable. We also use Pn and Qn to denote the classes of groups having these properties. Making use of the obvious inclusions, we define

Type
Research Article
Information
Canadian Journal of Mathematics , Volume 41 , Issue 2 , 01 April 1989 , pp. 369 - 384
Copyright
Copyright © Canadian Mathematical Society 1989

References

1. Bianchi, M., Brandi, R. and Mauri, A.G.B., On the 4-permutational property for groups, Arch. Math. (Basel) 48 (1987), 281–285.Google Scholar
2. Blyth, R.D., Rewriting products of group elements I, J. Algebra 116 (1988), 506–521.Google Scholar
3. Blyth, R.D., Rewriting products of group elements II, J. Algebra 118 (1988), 246–259.Google Scholar
4. Blyth, R.D. and Robinson, D.J.S., Recent progress on rewritability in groups, Proceedings of the 1987 Singapore Group Theory conference, to appear.Google Scholar
5. Brandl, R., General bounds for permutability in finite groups, preprint.Google Scholar
6. Curzio, M., Longobardi, P. and Maj, M., Su di un problema combinatorio in teoria dei gruppi, Atti. Accad. Naz. Lincei Rend. Cl. Sci. Fis. Mat. Natur. (8) 74 (1983), 136–142.Google Scholar
7. Curzio, M., Longobardi, P., Maj, M. and Robinson, D.J.S., A permutational property of groups, Arch. Math. (Basel) 44 (1985), 385–389.Google Scholar
8. Longobardi, P. and Maj, M., On groups in which every product of four elements can be reordered, Arch. Math. (Basel) 49 (1987), 273–276.Google Scholar
9. Longobardi, P. and Maj, M., On the derived length of groups with some permutational properties, preprint.Google Scholar
10. Longobardi, P., Maj, M. and Stonehewer, S.E., The classification of groups in which every product of four elements can be reordered, preprint.Google Scholar
11. Neumann, B.H., Groups covered by finitely many cosets, Publ. Math. Debrecen 3 (1954), 227- 242.Google Scholar
12. Restivo, A. and Reutenauer, C., On the Burnside problem for semigroups, J. Algebra 89 (1984), 102–104.Google Scholar
13. Robinson, D.J.S., Finiteness conditions and generalized soluble groups, Part I, Ergebnisse der Mathematik und ihrer Grenzgebiete, Band 62 (Springer-Verlag, Berlin, 1972).Google Scholar
14. Robinson, D.J.S., A course in the theory of groups, Graduate Texts in Mathematics, 80 (Springer-Verlag, New York-Berlin, 1982).Google Scholar
15. Tomkinson, M.J., FC-groups, Research Notes in Mathematics 96 (Pitman, London, 1984).Google Scholar