Hostname: page-component-78c5997874-xbtfd Total loading time: 0 Render date: 2024-11-05T04:14:45.815Z Has data issue: false hasContentIssue false
  • English
  • Français

Revisiting Tietze–Nakajima: Local and Global Convexity for Maps

Published online by Cambridge University Press:  20 November 2018

Christina Bjorndahl  and
Yael Karshon
Christina Bjorndahl*
Affiliation:
Department of Mathematics, University of Toronto, Toronto, ON M5S 2E4, CANADA
Yael Karshon*
Affiliation:
Department of Mathematics, University of Toronto, Toronto, ON M5S 2E4, CANADA
*
[email protected]
[email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

A theorem of Tietze and Nakajima, from 1928, asserts that if a subset 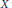$X$ of 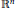${{\mathbb{R}}^{n}}$ is closed, connected, and locally convex, then it is convex. We give an analogous “local to global convexity” theorem when the inclusion map of 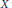$X$ to 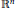${{\mathbb{R}}^{n}}$ is replaced by a map from a topological space 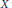$X$ to 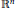${{\mathbb{R}}^{n}}$ that satisfies certain local properties. Our motivation comes from the Condevaux–Dazord–Molino proof of the Atiyah–Guillemin–Sternberg convexity theorem in symplectic geometry.

Keywords

53D2052B99
Type
Research Article
Information
Canadian Journal of Mathematics , Volume 62 , Issue 5 , 01 October 2010 , pp. 975 - 993
Copyright
Copyright © Canadian Mathematical Society 2010

Footnotes

*

Formerly Christina Marshall.

The first author is partially supported by an NSERC Discovery grant. The second author was partially funded by an NSERC USRA grant in the summers of 2004 and 2005.

References

[At] Atiyah, M., Convexity and commuting Hamiltonians. Bull. London Math. Soc. 14(1982), no. 1, 1–15. doi:10.1112/blms/14.1.1Google Scholar
[Be] Benoist, Y., Actions symplectiques de groupes compacts. Geom. Dedicata 89(2002), 181–245.Google Scholar
[BOR1] Birtea, P., Ortega, J-P., and Ratiu, T. S., Openness and convexity for momentum maps. Trans. Amer. Math. Soc. 361(2009), no. 2, 603–630. doi:10.1090/S0002-9947-08-04689-8Google Scholar
[BOR2] Birtea, P., A local-to-global principle for convexity in metric spaces. J. Lie Theory 18(2008), no. 2, 445–469.Google Scholar
[BF] Blumenthal, L. M. and Freese, R.W., Local convexity in metric spaces. Math. Notae 18(1962), 15–22.Google Scholar
[C] Cel, J., A generalization of Tietze's theorem on local convexity for open sets. Bull. Soc. Roy. Sci. Liège 67(1998), no. 1–2, 31–33.Google Scholar
[CD M] Condevaux, M., Dazord, P., and Molino, P., Géométrie du moment. In: Travaux du Séminaire Sud-Rhodanien de Géométrie, I, Publ. Dép. Math. Nouvelle Sér. B, 88-1, Univ. Claude-Bernard, Lyon, 1988, pp. 131–160.Google Scholar
[GS1] Guillemin, V. and Sternberg, S., Convexity properties of the moment mapping. Invent. Math. 67(1982), no. 3, 491–513. doi:10.1007/BF01398933Google Scholar
[GS2] Guillemin, V. and Sternberg, S., A normal form for the moment map. in: Differential geometric methods in mathematical physics (Jerusalem, 1982), Math. Phys. Stud., 6, Reidel, Dordrecht, 1984. pp. 161–175.Google Scholar
[HNP] Hilgert, J., Neeb, K.-H., and Plank, W., Symplectic convexity theorems. Sem. Sophus Lie 3(1993), no. 2, 123–135.Google Scholar
[Ka] Kay, D. C., Generalizations of Tietze's theorem on local convexity for sets in Rd. In: Discrete geometry and convexity (New York, 1982), Ann. New York Acad. Sci., 440, New York Acad. Sci., New York, 1985, pp. 179–191.Google Scholar
[KW] Kelly, P. J. and Weiss, M. L., Geometry and convexity: a study of mathematical methods. In: Pure and applied mathematics, John Wiley and Sons, Wiley-Interscience, New York, 1979.Google Scholar
[Kl] Klee, V. L., Jr., Convex sets in linear spaces. Duke Math. J. 18(1951), 443–466. doi:10.1215/S0012-7094-51-01835-2Google Scholar
[Kn] Knop, F., Convexity of Hamiltonian manifolds. J. Lie Theory 12(2002), no. 2, 571–582.Google Scholar
[N] Nakajima, S., Über konvexe Kurven and Flächen”. Tôhoku Math. J. 29(1928), 227–230.Google Scholar
[SSV] Sacksteder, R., Straus, E. G., and Valentine, F. A., A generalization of a theorem of Tietze and Nakajima on Local Convexity. J. London Math. Soc. 36(1961), 52–56. doi:10.1112/jlms/s1-36.1.52Google Scholar
[S] Schoenberg, I. J., On local convexity in Hilbert space. Bull. Amer. Math. Soc. 48(1942), 432–436. doi:10.1090/S0002-9904-1942-07693-2Google Scholar
[Ta] Takayuki, T., On a relation between local convexity and entire convexity. J. Sci. Gakugei Fac. Tokushima Univ. 1(1950), 25–30.Google Scholar
[Ti] Tietze, H., Über Konvexheit im kleinen und im großen und über gewisse den Punkter einer Menge zugeordete Dimensionszahlen. Math. Z. 28(1928), no. 1, 697–707. doi:10.1007/BF01181191Google Scholar