Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Gil, Juan B.
Krainer, Thomas
and
Mendoza, Gerardo A.
2006.
Resolvents of elliptic cone operators.
Journal of Functional Analysis,
Vol. 241,
Issue. 1,
p.
1.
Gil, Juan B.
Krainer, Thomas
and
Mendoza, Gerardo A.
2007.
Geometry and Spectra of Closed Extensions of Elliptic Cone Operators.
Canadian Journal of Mathematics,
Vol. 59,
Issue. 4,
p.
742.
Coriasco, S.
Schrohe, E.
and
Seiler, J.
2007.
BoundedH∞-Calculus for Differential Operators on Conic Manifolds with Boundary.
Communications in Partial Differential Equations,
Vol. 32,
Issue. 2,
p.
229.
Gil, Juan B.
Krainer, Thomas
and
Mendoza, Gerardo A.
2007.
Modern Trends in Pseudo-Differential Operators.
Vol. 172,
Issue. ,
p.
33.
Kirsten, Klaus
Loya, Paul
and
Park, Jinsung
2008.
Exotic Expansions and Pathological Properties of ζ-Functions on Conic Manifolds.
Journal of Geometric Analysis,
Vol. 18,
Issue. 3,
p.
835.
Gil, Juan B.
and
Loya, Paul A.
2008.
Resolvents of cone pseudodifferential operators, asymptotic expansions and applications.
Mathematische Zeitschrift,
Vol. 259,
Issue. 1,
p.
65.
Roidos, Nikolaos
and
Schrohe, Elmar
2013.
The Cahn-Hilliard Equation and the Allen-Cahn Equation on Manifolds with Conical Singularities.
Communications in Partial Differential Equations,
Vol. 38,
Issue. 5,
p.
925.
Roidos, Nikolaos
and
Schrohe, Elmar
2014.
Bounded imaginary powers of cone differential operators on higher order Mellin–Sobolev spaces and applications to the Cahn–Hilliard equation.
Journal of Differential Equations,
Vol. 257,
Issue. 3,
p.
611.
Roidos, Nikolaos
and
Schrohe, Elmar
2016.
Existence and maximalLp-regularity of solutions for the porous medium equation on manifolds with conical singularities.
Communications in Partial Differential Equations,
Vol. 41,
Issue. 9,
p.
1441.
Roidos, Nikolaos
2018.
Complex powers for cone differential operators and the heat equation on manifolds with conical singularities.
Proceedings of the American Mathematical Society,
Vol. 146,
Issue. 7,
p.
2995.
Schrohe, E.
and
Seiler, J.
2018.
Bounded
$$H_\infty $$
H
∞
-calculus for cone differential operators.
Journal of Evolution Equations,
Vol. 18,
Issue. 3,
p.
1395.
Roidos, Nikolaos
and
Schrohe, Elmar
2018.
Smoothness and long time existence for solutions of the porous medium equation on manifolds with conical singularities.
Communications in Partial Differential Equations,
Vol. 43,
Issue. 10,
p.
1456.
Nguyen, Nhu Thang
and
Nguyen, Thi Thu Huong
2019.
Multiple solutions for semilinear cone elliptic equations without Ambrosetti–Rabinowitz condition.
Journal of Pseudo-Differential Operators and Applications,
Vol. 10,
Issue. 3,
p.
747.
Lopes, Pedro T. P.
and
Schrohe, Elmar
2019.
Spectral Invariance of Pseudodifferential Boundary Value Problems on Manifolds with Conical Singularities.
Journal of Fourier Analysis and Applications,
Vol. 25,
Issue. 3,
p.
1147.
Roidos, Nikolaos
2020.
The Swift-Hohenberg equation on conic manifolds.
Journal of Mathematical Analysis and Applications,
Vol. 481,
Issue. 2,
p.
123491.
Roidos, Nikolaos
2020.
Conic manifolds under the Yamabe flow.
Journal of Evolution Equations,
Vol. 20,
Issue. 2,
p.
321.
Roidos, Nikolaos
Schrohe, Elmar
and
Seiler, Jörg
2021.
Bounded H∞-calculus for boundary value problems on manifolds with conical singularities.
Journal of Differential Equations,
Vol. 297,
Issue. ,
p.
370.
Nguyen, Thi Thu Huong
and
Nguyen, Nhu Thang
2021.
Existence and nonexistence of solutions to cone elliptic equations via Galerkin method.
Mathematische Nachrichten,
Vol. 294,
Issue. 10,
p.
1932.
Lopes, Pedro T. P.
and
Roidos, Nikolaos
2022.
Smoothness and long time existence for solutions of the Cahn–Hilliard equation on manifolds with conical singularities.
Monatshefte für Mathematik,
Vol. 197,
Issue. 4,
p.
677.
Wei, Yawei
2022.
Existence of multiple solutions for quasi-linear degenerate elliptic equations.
Science China Mathematics,
Vol. 65,
Issue. 5,
p.
971.
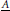 $\underset{\scriptscriptstyle-}{A}$ of an elliptic differential operator
$\underset{\scriptscriptstyle-}{A}$ of an elliptic differential operator  $A$ on a manifold with conical singularities, acting as an unbounded operator on a weighted
$A$ on a manifold with conical singularities, acting as an unbounded operator on a weighted 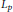 ${{L}_{p}}$-space. Under suitable conditions we show that the resolvent
${{L}_{p}}$-space. Under suitable conditions we show that the resolvent 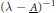 ${{\left( \lambda -\underset{\scriptscriptstyle-}{A} \right)}^{-1}}$ exists in a sector of the complex plane and decays like
${{\left( \lambda -\underset{\scriptscriptstyle-}{A} \right)}^{-1}}$ exists in a sector of the complex plane and decays like 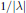 $1/\left| \lambda \right|$ as
$1/\left| \lambda \right|$ as 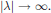 $\left| \lambda \right|\to \infty $. Moreover, we determine the structure of the resolvent with enough precision to guarantee existence and boundedness of imaginary powers of
$\left| \lambda \right|\to \infty $. Moreover, we determine the structure of the resolvent with enough precision to guarantee existence and boundedness of imaginary powers of 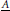 $\underset{\scriptscriptstyle-}{A}$.
$\underset{\scriptscriptstyle-}{A}$.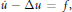 $\dot{u}\,-\,\Delta u\,=\,f,$
$\dot{u}\,-\,\Delta u\,=\,f,$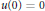 $u\left( 0 \right)\,=\,0$.
$u\left( 0 \right)\,=\,0$.

