Hostname: page-component-cd9895bd7-q99xh Total loading time: 0 Render date: 2024-12-26T00:46:05.588Z Has data issue: false hasContentIssue false
  • English
  • Français

Resolvent Means and InvertingGeneralized Fourier Transforms

Published online by Cambridge University Press:  20 November 2018

Louise A. Raphael
Louise A. Raphael*
Affiliation:
Howard University, Washington, D.C.
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let S-L denote a singular Sturm-Liouville system on the half line with homogeneous boundary conditions, possessing a discrete negative and continuous positive spectrum. Let A be the S-L operator and Sα(f; x) the S-L eigenfunction expansion associated with the resolvent operator (z – A)–1, z complex. That is, Sα(f; x) denotes the resolvent summability means with weight function z(z – λ)–1 (or (1 + tλ)–1 where t = – 1/z).

We first study the problem of determining when

(1)

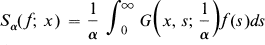
where 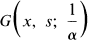is the Green's function associated with a certain perturbation of our system.

Type
Research Article
Information
Canadian Journal of Mathematics , Volume 38 , Issue 4 , 01 August 1986 , pp. 861 - 877
Copyright
Copyright © Canadian Mathematical Society 1986

References

1. Bochner, S. and Chandraskharan, K., Fourier transforms (Princeton University Press, Princeton, 1949).Google Scholar
2. Diamond, H., Kon, M. and Raphael, L. A., Stable summation methods for a class of singular Sturm-Liouville expansions, PAMS 81 (1981), 279–286.Google Scholar
3. Gurarie, D. and Kon, M., Radial bounds for perturbations of elliptic operators, J. Functional Analysis 56 (1984), 99–123.Google Scholar
4. Gurarie, D. and Kon, M., Resolvents and regularity properties of elliptic operators, Operator Theory: Advances and Applications (Birkhauser, Basel, 1983), 151–162.Google Scholar
5. Hille, E., Lectures on ordinary differential equations (Addison-Wesley, MA., 1969).Google Scholar
6. Hoffman, K. M., Banach spaces of analytic functions (Princeton Hall, New Jersey, 1962).Google Scholar
7. Kon, M. and Raphael, L. A., New multiplier methods for summing classical eigenfunction expansions, JDE 50 (1983), 391–406.Google Scholar
8. Levitan, B. M. and Sargsjan, I. S., Introduction to spectral theory: self adjoint ordinary differential operators, AMS (1975).CrossRefGoogle Scholar
9. Raphael, L. A., The Stieltjes summability method and summing Sturm-Liouville expansions, SIAM Book on Mathematical Analysis 13 (1982).Google Scholar
10. Raphael, L. A., Equisummability of eigenfunction expansions under analytic multipliers, J. Mathematical Analysis and Applications (to appear).CrossRefGoogle Scholar
11. Sadosky, C., Interpolation of operators and singular integrals (Marcel Dekker, New York, 1979).Google Scholar
12. Stein, E. M. and Weiss, G., Introduction to Fourier analysis on Euclidean spaces (Princeton University Press, Princeton, 1971).Google Scholar
13. Tikhonov, A. M. and Arsenin, V. Y., Solutions of ill-posed problems (V. H. Winston & Sons, Washington, D.C., 1977).Google Scholar
14. Titchmarsh, E. C., Eigenfunction expansions, Part I, Second Edition. (Oxford University Press, 1962); Part II (Oxford University Press, 1958).Google Scholar
15. Titchmarsh, E. C., Introduction to the theory of Fourier integrals (Oxford University Press, 1937).Google Scholar