Published online by Cambridge University Press: 20 November 2018
This paper is concerned with the residual spectrum of the hermitian quaternionic classical groups 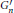 $G_{n}^{\prime }$ and
$G_{n}^{\prime }$ and 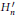 $H_{n}^{\prime }$ defined as algebraic groups for a quaternion algebra over an algebraic number field. Groups
$H_{n}^{\prime }$ defined as algebraic groups for a quaternion algebra over an algebraic number field. Groups 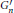 $G_{n}^{\prime }$ and
$G_{n}^{\prime }$ and 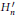 $H_{n}^{\prime }$ are not quasi-split. They are inner forms of the split groups
$H_{n}^{\prime }$ are not quasi-split. They are inner forms of the split groups  $\text{S}{{\text{O}}_{4n}}$ and
$\text{S}{{\text{O}}_{4n}}$ and 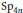 $\text{S}{{\text{p}}_{4n}}$. Hence, the parts of the residual spectrum of
$\text{S}{{\text{p}}_{4n}}$. Hence, the parts of the residual spectrum of 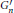 $G_{n}^{\prime }$ and
$G_{n}^{\prime }$ and 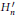 $H_{n}^{\prime }$ obtained in this paper are compared to the corresponding parts for the split groups
$H_{n}^{\prime }$ obtained in this paper are compared to the corresponding parts for the split groups  $\text{S}{{\text{O}}_{4n}}$ and
$\text{S}{{\text{O}}_{4n}}$ and 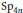 $\text{S}{{\text{p}}_{4n}}$.
$\text{S}{{\text{p}}_{4n}}$.