Article contents
Representations of Well-Founded Preference Orders
Published online by Cambridge University Press: 20 November 2018
Extract
A preference order, or linear preorder, on a set X is a binary relation 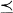 which is transitive, reflexive and total. This preorder partitions the set X into equivalence classes of the form
which is transitive, reflexive and total. This preorder partitions the set X into equivalence classes of the form 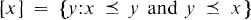 . The natural relation induced by
. The natural relation induced by 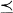 on the set of equivalence classes is a linear order. A well-founded preference order, or prewellordering, will similarly induce a well-ordering. A representation or Paretian utility function of a preference order is an order-preserving map f from X into the R of real numbers (provided with the standard ordering). Mathematicians and economists have studied the problem of obtaining continuous or measurable representations of suitably defined preference orders [4, 7]. Parametrized versions of this problem have also been studied [1, 7, 8]. Given a continuum of preference orders which vary in some reasonable sense with a parameter t, one would like to obtain a continuum of representations which similarly vary with t.
on the set of equivalence classes is a linear order. A well-founded preference order, or prewellordering, will similarly induce a well-ordering. A representation or Paretian utility function of a preference order is an order-preserving map f from X into the R of real numbers (provided with the standard ordering). Mathematicians and economists have studied the problem of obtaining continuous or measurable representations of suitably defined preference orders [4, 7]. Parametrized versions of this problem have also been studied [1, 7, 8]. Given a continuum of preference orders which vary in some reasonable sense with a parameter t, one would like to obtain a continuum of representations which similarly vary with t.
- Type
- Research Article
- Information
- Copyright
- Copyright © Canadian Mathematical Society 1983
References
- 2
- Cited by


