Hostname: page-component-cd9895bd7-gxg78 Total loading time: 0 Render date: 2024-12-26T00:40:25.506Z Has data issue: false hasContentIssue false
  • English
  • Français

Representations of Virasoro-Heisenberg Algebras and Virasoro-Toroidal Algebras

Published online by Cambridge University Press:  20 November 2018

Marc A. Fabbri  and
Frank Okoh
Marc A. Fabbri
Affiliation:
Department of Mathematics, Arizona State University, Tempe, Arizona 85287, U.S.A.
Frank Okoh
Affiliation:
Department of Mathematics, Wayne State University, Detroit, Michigan 48202, U.S.A.
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Virasoro-toroidal algebras, 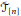${{\tilde{J}}_{[n]}}$, are semi-direct products of toroidal algebras 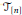${{J}_{[n]}}$ and the Virasoro algebra. The toroidal algebras are, in turn, multi-loop versions of affine Kac-Moody algebras. Let $\Gamma $ be an extension of a simply laced lattice 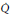$\dot{Q}$ by a hyperbolic lattice of rank two. There is a Fock space 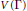$V\left( \Gamma \right)$ corresponding to $\Gamma $ with a decomposition as a complex vector space: 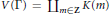$V\left( \Gamma \right)=\coprod{_{m\in z}K\left( m \right)}$ . Fabbri and Moody have shown that when 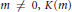$m\ne 0,\,K\left( m \right)$ is an irreducible representation of 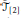${{\tilde{J}}_{[2]}}$ . In this paper we produce a filtration of 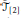${{\tilde{J}}_{[2]}}$-submodules of 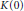$K\left( 0 \right)$. When $L$ is an arbitrary geometric lattice and $n$ is a positive integer, we construct a Virasoro-Heisenberg algebra 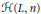$\tilde{H}\left( L,n \right)$ . Let 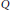$Q$ be an extension of 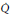$\dot{Q}$ by a degenerate rank one lattice. We determine the components of 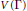$V\left( \Gamma \right)$ that are irreducible 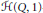$\tilde{H}\left( Q,1 \right)$ -modules and we show that the reducible components have a filtration of 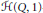$\tilde{H}\left( Q,1 \right)$-submodules with completely reducible quotients. Analogous results are obtained for 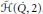$\tilde{H}\left( \dot{Q},2 \right)$ . These results complement and extend results of Fabbri and Moody.

Keywords

17B6517B68
Type
Research Article
Information
Canadian Journal of Mathematics , Volume 51 , Issue 3 , 01 June 1999 , pp. 523 - 545
Copyright
Copyright © Canadian Mathematical Society 1999

References

[BC] Berman, S. and Cox, A., Enveloping algebras and representations of toroidal Lie algebras. Pacific J. Math. 165 (1994), 239–267.Google Scholar
[BO] Borcherds, R., Vertex algebras, Kac-Moody algebras and theMonster. Proc. Nat. Acad. Sci. U.S.A. 83 (1986), 3068–3071.Google Scholar
[COL] Coleman, A. J., Groups and Physics. Notices Amer.Math. Soc. 44 (1997), 8–17.Google Scholar
[E1] Eswara Rao, S., Iterated loop modules and a filtration for vertex representations of toroidal Lie algebras. Pacific J. Math. 171 (1995), 511–528.Google Scholar
[E2] Eswara Rao, S., Classification of loop modules with finite dimensional weight spaces. Math. Ann. 305 (1996), 651–663.Google Scholar
[EM] Eswara Rao, S. and Moody, R. V., Vertex representations for the universal central extensions for the n-toroidal Lie algebras and a generalization of the Virasoro algebra. Comm. Math. Phys. 159 (1994), 239–266.Google Scholar
[F] Fabbri, M. A., Virasoro-toroidal algebras and vertex representations. C. R. Math. Rep. Acad. Sci. Canada 14 (1992), 77–82.Google Scholar
[M] Fabbri, M. A. and Moody, R. V., Irreducible representations of Virasoro-toroidal Lie algebras. Comm.Math. Phys. 159 (1994), 1–13.Google Scholar
[FK] Frenkel, I. and Kac, V. G., Basic representations of affine Lie algebras and dual resonance model. Invent. Math.. 63 (1980), 23–66.Google Scholar
[FLM] Frenkel, I., Lepowsky, J. and Meurman, A., Vertex operator algebras and the monster. Academic Press, 1988.Google Scholar
[GO] Goddard, P. and Olive, D., Algebras, lattices, and strings. In: Vertex operators in Mathematics and Physics (eds. Lepowsky, J., Mandelstram, S. and Singer, I.M.),MSRI Berkeley Publication 3, Berkeley, California, 1984, 51–96.Google Scholar
[KR] Kac, V. G. and Raina, A. K., Bombay Lectures on Highest Weight Representations of Infinite-Dimensional Lie Algebras. SingaporeWorld Scientific, 1987.Google Scholar
[KS] Kassel, C., Kähler differentials and coverings of complex simple Lie algebras extended over a commutative algebra. J. Pure Appl. Algebra 34 (1985), 265–275.Google Scholar
[MEY] Moody, R. V., Eswara Rao, S. and Yokonuma, T., Toroidal Lie algebras and vertex representations. Geom. Dedicata 35 (1990), 283–307.Google Scholar
[MP1] Moody, R. V. and Pianzola, A., Infinite-dimensional Lie algebras (a unifying overview). Algebras Groups Geom. 4 (1987), 211–230.Google Scholar
[MP2] Moody, R. V. and Pianzola, A., Lie Algebras with triangular decomposition. J.Wiley, 1995.Google Scholar
[Z] Zhang, H., A class of representations over the Virasoro algebra. J. Algebra 190 (1997), 1–10.Google Scholar