Published online by Cambridge University Press: 20 November 2018
A Lie algebra 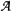 is called a Heisenberg algebra if its centre coincides with its derived algebra and is one-dimensional. When
is called a Heisenberg algebra if its centre coincides with its derived algebra and is one-dimensional. When 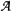 is infinite-dimensional, Kac, Kazhdan, Lepowsky, and Wilson have proved that
is infinite-dimensional, Kac, Kazhdan, Lepowsky, and Wilson have proved that 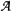 -modules that satisfy certain conditions are direct sums of a canonical irreducible submodule. This is an algebraic analogue of the Stone-von Neumann theorem. In this paper, we extract quantum Heisenberg algebras,
-modules that satisfy certain conditions are direct sums of a canonical irreducible submodule. This is an algebraic analogue of the Stone-von Neumann theorem. In this paper, we extract quantum Heisenberg algebras, 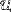 q(
q(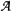 ), from the quantum affine algebras whose vertex representations were constructed by Frenkel and Jing. We introduce the canonical irreducible
), from the quantum affine algebras whose vertex representations were constructed by Frenkel and Jing. We introduce the canonical irreducible 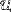 q(
q(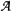 )-module Mq and a class Cq of
)-module Mq and a class Cq of 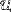 q(
q(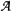 )-modules that are shown to have the Stone-von Neumann property. The only restriction we place on the complex number q is that it is not a square root of 1. If q1 and q2 are not roots of unity, or are both primitive m-th roots of unity, we construct an explicit isomorphism between
)-modules that are shown to have the Stone-von Neumann property. The only restriction we place on the complex number q is that it is not a square root of 1. If q1 and q2 are not roots of unity, or are both primitive m-th roots of unity, we construct an explicit isomorphism between 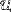 q1(
q1(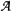 ) and
) and 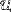 q2(
q2(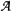 ). If q1 is a primitive m-th root of unity, m odd, q2 a primitive 2m-th or a primitive 4m-th root of unity, we also construct an explicit isomorphism between
). If q1 is a primitive m-th root of unity, m odd, q2 a primitive 2m-th or a primitive 4m-th root of unity, we also construct an explicit isomorphism between 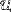 q1(
q1(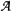 ) and
) and 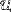 q2(
q2(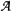 ).
).