Hostname: page-component-586b7cd67f-t8hqh Total loading time: 0 Render date: 2024-11-20T16:20:56.519Z Has data issue: false hasContentIssue false
  • English
  • Français

Representations of Foundation Semigroups and their Algebras

Published online by Cambridge University Press:  20 November 2018

M. Lashkarizadeh Bami
M. Lashkarizadeh Bami*
Affiliation:
University of Isfahan, Isfahan, Iran
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

The aim of this paper is to extend to a suitable class of topological semigroups parts of well-defined theory of representations of topological groups. In attempting to obtain these results it was soon realized that no general theory was likely to be obtainable for all locally compact semigroups. The reason for this is the absence of any analogue of the group algebra Ll(G). So the theory in this paper is restricted to a certain family of topological semigroups. In this account we shall only give the details of those parts of proofs which depart from the standard proofs of analogous theorems for groups.

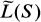On a locally compact semigroup S the algebra of all μ ∊ M(S) for which the mapping 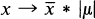and 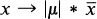of S to M(S) (where 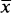denotes the point mass at x) are continuous when M(S) has the weak topology was first studied in the sequence of papers [1, 2, 3] by A. C. and J. W. Baker.

Type
Research Article
Information
Canadian Journal of Mathematics , Volume 37 , Issue 1 , 01 February 1985 , pp. 29 - 47
Copyright
Copyright © Canadian Mathematical Society 1985

References

1. Baker, A. C. and Baker, J. W., Algebras of measures on a locally compact semigroup, J. London Math. Soc. (2) 1 (1969), 249–259.Google Scholar
2. Baker, A. C. and Baker, J. W., Algebras of measures on a locally compact semigroup II, J. London Math. Soc. (2) (1970), 651–659.Google Scholar
3. Baker, A. C. and Baker, J. W., Algebras of measures on a locally compact semigroup III, J. London Math. Soc. (2) 4 (1972), 685–695.Google Scholar
4. Bonsall, F. and Duncan, J., Complete normed algebras (Springer-Verlag, Heidelberg, 1973).CrossRefGoogle Scholar
5. Edwards, R. E., Functional analysis, theory and applications (Holt, Reinhart and Winstone, New York, 1965).Google Scholar
6. Halmos, P., Measure theory (Springer-Verlag, Heidelberg, 1974).Google Scholar
7. Hewitt, E. and Ross, K. A., Abstract harmonic analysis I (Springer-Verlag, Heidelberg, 1970).Google Scholar
8. Rudin, W., Real and complex analysis (Tata-McGraw Hill, 1974).Google Scholar
9. Sakai, S., C*-algebras and W*-algebras (Springer-Verlag, Heidelberg, 1971).Google Scholar
10. Sleijpen, G. L. G., Locally compact semigroups and continuous translations of measures, Proc. London Math. Soc. (3) 37 (1978), 75–79.Google Scholar