Hostname: page-component-586b7cd67f-dsjbd Total loading time: 0 Render date: 2024-11-22T14:38:13.971Z Has data issue: false hasContentIssue false
  • English
  • Français

Regulators of an Infinite Family of theSimplest Quartic Function Fields

Published online by Cambridge University Press:  20 November 2018

Jungyun Lee  and
Yoonjin Lee
Jungyun Lee
Affiliation:
Institute of Mathematical Sciences, EwhaWomans University, 52, Ewhayeodae-gil, Seodaemun-gu, Seoul 03760, Republic of Korea e-mail: [email protected]
Yoonjin Lee
Affiliation:
Department of Mathematics, Ewha Womans University, 52, Ewhayeodae-gil, Seodaemun-gu, Seoul 03760, Republic of Korea e-mail: [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

We explicitly find regulators of an infinite family 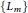$\{{{L}_{m}}\}$ of the simplest quartic function fields with a parameter $m$ in a polynomial ring 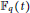${{\mathbb{F}}_{q}}\left( t \right)$, where 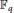${{\mathbb{F}}_{q}}$ is the finite field of order $q$ with odd characteristic. In fact, this infinite family of the simplest quartic function fields are subfields of maximal real subfields of cyclotomic function fields having the same conductors. We obtain a lower bound on the class numbers of the family 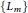$\{{{L}_{m}}\}$ and some result on the divisibility of the divisor class numbers of cyclotomic function fields that contain 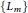$\{{{L}_{m}}\}$ as their subfields. Furthermore, we find an explicit criterion for the characterization of splitting types of all the primes of the rational function field 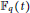${{\mathbb{F}}_{q}}\left( t \right)$ in 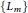$\{{{L}_{m}}\}$.

Keywords

11R2911R58regulatorfunction fieldquartic extensionclass number
Type
Research Article
Information
Canadian Journal of Mathematics , Volume 69 , Issue 3 , 01 June 2017 , pp. 579 - 594
Copyright
Copyright © Canadian Mathematical Society 2017

References

[1] Bae, S., Real quadratic function fields of Richaud-Degert type with ideal class number one. Proc. Amer. Soc. Math. 140(2011), no. 2, 403–414.http://dx.doi.org/10.1090/S0002-9939-2011-10910-9 Google Scholar
[2] Cassels, J. W. S., An introduction to the geometry of numbers. Springer-Verlag, Berlin, 1971.Google Scholar
[3] Feng, K. and Hu, W., On real quadratic function fields of Chowla type with ideal class number one. Proc. Amer. Soc. Math. 127(1999), no. 5,1301–1307.http://dx.doi.org/10.1090/S0002-9939-99-05004-2 Google Scholar
[4] Gras, M-N., Table numérique du nombre de classes et des unités des extensions cycliques réelles de degré 4 de ℚ. Publ. Math. Fac. Sci. Besançon, Théorie des Nombres, Fasc. 2, (1977/78) 1–53.Google Scholar
[5] Gras, M-N., Special units in real cyclic sextic fields. Math. Comp. 48(1987), no. 177,179–182.http://dx.doi.org/10.1090/S0025-5718-1987-0866107-1 Google Scholar
[6] Guo, L. and Shu, L., Class numbers of cyclotomic function fields. Trans. Amer. Math. Soc. 351(1999), no. 11, 4445–4467. http://dx.doi.org/10.1090/S0002-9947-99-02325-9 Google Scholar
[7] Haghighi, M., Computation of conductor for finite extensions with cyclic Galois groups. J. Algebra 124(1989), no. 2, 329–333.http://dx.doi.org/10.101 6/0021-8693(89)90134-8 Google Scholar
[8] Hasse, H., Arithmetische Bestimmung von Grundeinheit und Klassenzahl in zyklischen kubischen und biquadratischen Zahlkörpern, Mathematische Abhandlungen. Band 3, Walter de Gruyter, Berlin, 1975, pp. 290–379.Google Scholar
[9] Im, B-H. and Lee, Y., Decomposition of places in dihedral and cyclic quintic trinomial extensions of global fields. Manuscripta Math. 137(2012), no. 1-2,107–127.http://dx.doi.org/10.1007/s00229-011-0459-4 Google Scholar
[10] Kishi, Y., A family of cyclic cubic polynomials whose roots are systems of fundamental units. J. Number Theory 102(2003), no. 1, 90–106.http://dx.doi.Org/10.1016/S0022-314X(03)00085-4 Google Scholar
[11] Lazarus, A. J., On the class number and unit index of simplest quartic fields. Nagoya Math. J. 121(1991), 1–13.http://dx.doi.org/10.1017/S0027763000003378 Google Scholar
[12] Lee, Y., Scheidler, R., and Yarrish, C., Computation of the fundamental units and the regulator of a cyclic cubic function field. Experiment. Math. 12(2003), no. 2, 211–225.http://dx.doi.org/10.1080/10586458.2003.10504493 Google Scholar
[13] Lehmer, E., Connection between Gaussian periods and cyclic units. Math. Comp. 50(1988), no. 182, 535–541.http://dx.doi.org/10.1090/S0025-5718-1988-0929551-0 Google Scholar
[14] Louboutin, S. R., Hasse unit indices of dihedral octic CM-fields. Math. Nachr. 215(2000), 107–113.http://dx.doi.Org/10.1002/1522-2616(200007)215:1<107::AID-MANA107>3.0.CO;2-</107::AID-MANA107> 3.0.CO;2->Google Scholar
[15] Louboutin, S. R., The simplest quartic fields with ideal class groups of exponents less than or equal to 2. J. Math. Soc. Japan 56(2004), no. 3, 717–727.http://dx.doi.Org/10.2969/jmsj71191334082 Google Scholar
[16] Rosen, M., Number theory in function fields. Graduate Texts in Mathematics, 210. Springer-Verlag, New York, 2002.http://dx.doi.Org/10.1007/978-1-4757-6046-0, Google Scholar
[17] Scheidler, R. and Stein, A., Approximating Euler products and class number computation in algebraic function fields. Rocky Mountain J. Math. 40(2010), no. 5,1689–1727.http://dx.doi.Org/10.1216/RMJ-2O10-40-5-1689 Google Scholar
[18] Schoof, R. and Washington, L. C., Quintic polynomials and real cyclotomic fields with large class numbers. Math. Comp. 50(1988), no. 182, 543–556.http://dx.doi.Org/10.2307/2008623 Google Scholar
[19] Shen, Y. Y, Unit groups and class numbers of real cyclic octic fields. Trans. Amer. Math. Soc. 326(1991), no. 1, 179–209.http://dx.doi.org/10.1090/S0002-9947-1991-1031243-3 Google Scholar
[20] Stein, A. and Williams, H. C., Some methods for evaluating the regulator of a real quadratic function field. Experiment. Math. 8(1999), no. 2,119–133. http://dx.doi.org/10.1080/10586458.1999.10504394 Google Scholar
[21] Tomita, K. and Yamamuro, K., Lower bounds for fundamental units of real quadratic fields. Nagoya Math. J. 166(2002), 29–37.http://dx.doi.org/10.1017/S0027763000008230 Google Scholar
[22] Washington, L. C., A family of cyclic quartic fields arising from modular curves. Math. Comp. 57(1991), no. 196, 763–775.http://dx.doi.org/10.1090/S0025-5718-1991-1094964-6 Google Scholar
[23] Williams, H. C. and Zarnke, C. R., Computer calculation of units in cubic fields. Proceedings of the Second Manitoba Conference on Numerical Mathematics, Congressus Numerantium VII (1972), 433–468.Google Scholar
[24] Wu, Q. and Scheidler, R., An explicit treatment of biquadratic function fields. Contrib. Discrete Math. 2(2007), no. 1, 43–60.Google Scholar
[25] Zhang, Z.and Yue, Q., Fundamental units of real quadratic fields of odd class number. J. Number Theory 137(2014), 122–129.http://dx.doi.org/10.1016/j.jnt.2O13.10.019 Google Scholar