Hostname: page-component-cd9895bd7-7cvxr Total loading time: 0 Render date: 2024-12-26T00:43:41.940Z Has data issue: false hasContentIssue false
  • English
  • Français

Regularization of the Kepler Problem on the Three-sphere

Published online by Cambridge University Press:  20 November 2018

Shengda Hu  and
Manuele Santoprete
Shengda Hu
Affiliation:
Department of Mathematics, Wilfrid Laurier University, Waterloo, ON N2L 3C5. e-mail: [email protected] [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

In this paper we regularize the Kepler problem on 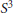${{S}^{3}}$ in several different ways. First, we perform a Moser-type regularization. Then, we adapt the Ligon–Schaaf regularization to our problem. Finally, we show that the Moser regularization and the Ligon–Schaaf map we obtained can be understood as the composition of the corresponding maps for the Kepler problem in Euclidean space and the gnomonic transformation.

Keywords

70FxxKepler problem on the sphereLigon-Shaaf regularizationgeodesic flow on the sphere
Type
Research Article
Information
Canadian Journal of Mathematics , Volume 66 , Issue 4 , 01 August 2014 , pp. 760 - 782
Copyright
Copyright © Canadian Mathematical Society 2014

Footnotes

*

The research of S. H. was supported by an NSERC Discovery Grant and a Wilfrid Laurier start-up grant. The research of M. S. was supported by NSERC through a Discovery Grant.

References

[1] Abraham, R. and Marsden, J. E., Foundations of mechanics. Second ed., revised and enlarged, Benjamin/Cummings Publishing Co., Inc., Advanced Book Program, Reading, Mass., 1978.Google Scholar
[2] Appell, P., Sur les lois de forces centrales faisant decrire á leur point d’application une conique quelles que soient les conditions initiales. Amer. J. Math. 13(1891), no. 2, 153–158. http://dx.doi.org/10.2307/2369811 CrossRefGoogle Scholar
[3] Cariñena, J. F., Rañada, M. F., and Santander, M., Central potentials on spaces of constant curvature: the Kepler problem on the two-dimensional sphere S2 and the hyperbolic plane H2. J. Math. Phys. 46(2005), no. 5, 052702. http://dx.doi.org/10.1063/1.1893214 CrossRefGoogle Scholar
[4] Cushman, R. H. and Duistermaat, J. J., A characterization of the Ligon–Schaaf regularization map. Comm. Pure Appl. Math. 50(1997), no. 8, 773–787. http://dx.doi.org/10.1002/(SICI)1097-0312(199708)50:8h773::AID-CPA3i3.0.CO;2-3 3.0.CO;2-3>CrossRefGoogle Scholar
[5] Cushman, R. H. and Bates, L. M., Global aspects of classical integrable systems. Birkhäuser Verlag, Basel, 1997.10.1007/978-3-0348-8891-2CrossRefGoogle Scholar
[6] Diacu, F., Pérez-Chavela, E., and Santoprete, M. The n-body problem in spaces of constant curvature. Part I: Relative equilibria. J. Nonlinear Sci. 22(2012), no. 2, 247–266. http://dx.doi.org/10.1007/s00332-011-9116-zCrossRefGoogle Scholar
[7] Diacu, F., The n-body problem in spaces of constant curvature. Part II: Singularities. J. Nonlinear Sci. 22(2012), no. 2, 267–275. http://dx.doi.org/10.1007/s00332-011-9117-y CrossRefGoogle Scholar
[8] Diacu, F., Relative equilibria in the curved n-body problem. Atlantis Studies in Dynamical Systems, Atlantis Press, 2012.Google Scholar
[9] Dirac, P. A. M., Generalized Hamiltonian dynamics. Canad. J. Math. 2(1950), 129–148. http://dx.doi.org/10.4153/CJM-1950-012-1 CrossRefGoogle Scholar
[10] Dirac, P. A. M., Lectures on quantum mechanics. Belfer Graduate School of Science Monographs Series, 2, Belfer Graduate School of Science, New York, 1967.Google Scholar
[11] Easton, R., Regularization of vector fields by surgery. J. Differential Equations 10(1971), 92–99. http://dx.doi.org/10.1016/0022-0396(71)90098-2 CrossRefGoogle Scholar
[12] Garcia-Gutierrez, L. and Santander, M., Levi-Civita regularization and geodesic flows for the ‘curved’ Kepler problem. http://arxiv:0707.3810v2. Google Scholar
[13] Goldstein, H., More on the prehistory of the Laplace or Runge-Lenz vector. Amer. J. Phys. 44(1976), 1123.10.1119/1.10202CrossRefGoogle Scholar
[14] G. Heckman and T. de Laat, On the regularization of the Kepler problem. http://arxiv:1007.3695. Google Scholar
[15] Higgs, P.W., Dynamical symmetries in a spherical geometry. I. J. Phys. A, 309(1979), no. 3, 309–323. http://dx.doi.org/10.1088/0305-4470/12/3/006 CrossRefGoogle Scholar
[16] Kustaanheimo, P. and Stiefel, E.. Perturbation theory of Kepler motion based on spinor regularization. J. Reine Angew. Math. 219(1965), 204–219.CrossRefGoogle Scholar
[17] Levi-Civita, T., Sur la régularisation du problème des trois corps. Acta Math. 42(1920), no. 1, 99–144. http://dx.doi.org/10.1007/BF02404404 CrossRefGoogle Scholar
[18] Ligon, T., and Schaaf, M., On the global symmetry of the classical Kepler problem. Rep. Mathematical Phys. 9(1976), no. 3, 281–300. http://dx.doi.org/10.1016/0034-4877(76)90061-6 CrossRefGoogle Scholar
[19] Marle, C.-M., A property of conformally Hamiltonian vector fields; application to the Kepler problem. http://arxiv:1011.5731. Google Scholar
[20] Milnor, J., On the geometry of the Kepler problem. Amer. Math. Monthly 90(1983), no. 6, 353–365. http://dx.doi.org/10.2307/2975570 CrossRefGoogle Scholar
[21] Moser, J., Regularization of Kepler's problem and the averaging method on a manifold. Comm. Pure Appl. Math. 23(1970), 609–636. http://dx.doi.org/10.1002/cpa.3160230406 CrossRefGoogle Scholar
[22] Santoprete, M., Gravitational and harmonic oscillator potentials on surfaces of revolution. J. Math. Phys. 49(2008), no. 4, 042903. http://dx.doi.org/10.1063/1.2912325 CrossRefGoogle Scholar
[23] Santoprete, M., Block regularization of the Kepler problem on surfaces of revolution with positive constant curvature. J. Differential Equations 247(2009), no. 4, 1043–1063. http://dx.doi.org/10.1016/j.jde.2009.05.003 CrossRefGoogle Scholar
[24] Serret, P., Théorie nouvelle géométrique et mécanique des lignes a double courbure. Mallet-Bachelier, Paris, 1860.Google Scholar
[25] Souriau, J. M., Géométrie globale du probléme á deux corps. Proceedings of the IUTAM-ISIMM symposium on modern developments in analytical mechanics. Vol. I (Torino, 1982). Atti Accad. Sci. Torino Cl. Sci. Fis. Mat. Natur. 117(1983), suppl. 1, 369–418.Google Scholar