Hostname: page-component-78c5997874-lj6df Total loading time: 0 Render date: 2024-11-16T15:05:01.667Z Has data issue: false hasContentIssue false
  • English
  • Français

Regular and Strongly Finitary Structures Over Strongly Algebroidal Categories

Published online by Cambridge University Press:  20 November 2018

Günter Matthiessen
Günter Matthiessen*
Affiliation:
Gesamthochschule Kassel/HRZ, Mönchebergstr. 19, 3500 Kassel, West Germany
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

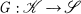Most properties an algebraist needs in categories are reflected by regular functors, introduced in [6]. If is a regular and strongly finitary functor and has some nice properties, it can be shown that the left adjoint functor of G helps to characterize finitary and strongly finitary objects of . The property of being algebroidal can be lifted from 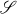to if a certain condition holds in 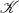. As an application, the implicational hull of subcategories can be constructed with the help of reduced products.

Type
Research Article
Information
Canadian Journal of Mathematics , Volume 30 , Issue 2 , 01 April 1978 , pp. 250 - 261
Copyright
Copyright © Canadian Mathematical Society 1978

References

1. Andréka, H., Marid, L., and Németi, I., Reduced products in categories, submitted to Journal of Pure and Applied Algebra.Google Scholar
2. Banaschewski, B. and Hérrlich, H., Subcategories defined by implications, Houston J. Math. 2 (1976).Google Scholar
3. Cohn, P. M., Universal algebra (Harper & Row, New York, 1965).Google Scholar
4. Fakir, S. and Haddad, L., Objets cohérents et ultraproduits dans les categories, J. Algebra 21 (1972), 410–421.Google Scholar
5. Gabriel, P. and Ulmer, F., Lokal pràsentierbare Kategorien, Lecture Notes in Mathematics 221 (1971).Google Scholar
6. Hérrlich, H., Regular categories and regular functors, Can. J. Math. 26 (1974), 709–720.Google Scholar
7. Hérrlich, H. and Strecker, G., Category theory (Boston, 1973).Google Scholar
8. Mal'cev, A. I., Algebraic systems (Springer-Verlag, Berlin-Heidelberg-New York, 1973).Google Scholar
9. Matthiessen, G., Théorie der heterogenen Algebren (Dissertation), Mathematik-Arbeitspapiere Nr. 3, Universitât Bremen (1976).Google Scholar