Hostname: page-component-cd9895bd7-gxg78 Total loading time: 0 Render date: 2024-12-26T01:08:02.207Z Has data issue: false hasContentIssue false
  • English
  • Français

Reducibility in Aℝ(K), Cℝ(K), and A(K)

Published online by Cambridge University Press:  20 November 2018

R. Rupp  and
A. Sasane
R. Rupp
Affiliation:
Fakultät Allgemeinwissenschaften, Georg-Simon-Ohm-Hochschule Nürnberg, D-90489 Nürnberg, Germany, e-mail: [email protected]
A. Sasane
Affiliation:
Fakultät Allgemeinwissenschaften, Georg-Simon-Ohm-Hochschule Nürnberg, D-90489 Nürnberg, Germany, e-mail: [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let 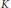$K$ denote a compact real symmetric subset of $\mathbb{C}$ and let 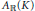${{A}_{\mathbb{R}}}\left( K \right)$ denote the real Banach algebra of all real symmetric continuous functions on 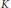$K$ that are analytic in the interior 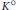${{K}^{\circ }}$ of 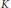$K$, endowed with the supremum norm. We characterize all unimodular pairs 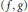$\left( f,\,g \right)$ in 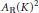${{A}_{\mathbb{R}}}{{\left( K \right)}^{2}}$ which are reducible. In addition, for an arbitrary compact 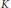$K$ in $\mathbb{C}$, we give a new proof (not relying on Banach algebra theory or elementary stable rank techniques) of the fact that the Bass stable rank of 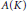$A\left( K \right)$ is 1. Finally, we also characterize all compact real symmetric sets 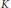$K$ such that 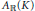${{A}_{\mathbb{R}}}\left( K \right)$, respectively 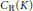${{C}_{\mathbb{R}}}\left( K \right)$, has Bass stable rank 1.

Keywords

46J1519B1030H0593D15real Banach algebrasBass stable ranktopological stable rankreducibility
Type
Research Article
Information
Canadian Journal of Mathematics , Volume 62 , Issue 3 , 01 June 2010 , pp. 646 - 667
Copyright
Copyright © Canadian Mathematical Society 2010

References

[1] Ahlfors, L. V., Complex Analysis. Third edition. Mc Graw-Hill, New York, 1978.Google Scholar
[2] Bass, H., K-theory and stable algebra. Inst. Hautes Études Sci. Publ. Math. 22(1964), 5–60.Google Scholar
[3] Burckel, R. B., An Introduction to Classical Complex Analysis, Vol. 1. Pure and Applied Mathematics 82. Academic Press, New York, 1979.Google Scholar
[4] Corach, G. and Larotonda, A. R., Stable range in Banach algebras. J, Pure Appl. Algebra 32(1984), 289–300. doi:10.1016/0022-4049(84)90093-8 Google Scholar
[5] Corach, G. and Suárez, F. D., Extension problems and stable rank in commutative Banach algebras. Topology Appl. 21(1985), no. 1, 1–8. doi:10.1016/0166-8641(85)90052-5 Google Scholar
[6] Corach, G. and Suárez, F. D., Stable rank in holomorphic function algebras. Illinois J. Math. 29(1985), no. 4, 627–639.Google Scholar
[7] Garnett, J. B., Bounded Analytic Functions. Pure and Applied Mathematics 96. Academic Press, New York, 1981.Google Scholar
[8] Gillman, L. and Jerison, M., Rings of Continuous Functions. van Nostrand, D., Princeton, NJ, 1960.Google Scholar
[9] Mortini, R. and Rupp, R., A constructive proof of the Nullstellensatz for subalgebras of A(K). In: Travaux mathématiques III. Sém. Math. Luxembourg, Centre Univ. Luxembourg, Luxembourg, 1991, pp. 45–49.Google Scholar
[10] Nagata, J., Modern Dimension Theory. Rev. edition. Sigma Series in Pure Mathematics 2. Heldermann Verlag, Berlin, 1983.Google Scholar
[11] Quadrat, A., On a general structure of the stabilizing controllers based on stable range. SIA M J. Control Optim. 42(2004), no. 6, 2264–2285. doi:10.1137/S0363012902408277 Google Scholar
[12] Rieffel, M. A., Dimension and stable rank in the K-theory of C∗-algebras. Proc. London Math. Soc. 46(1983), no.2, 301–333. doi:10.1112/plms/s3-46.2.301 Google Scholar
[13] Rupp, R., Stable rank in Banach algebras. In: Function Spaces. Lecture Notes in Pure and Appl. Math. 136. Dekker, New York, 1992, pp. 357–365.Google Scholar
[14] Rupp, R. and Sasane, A. J., On the stable rank and reducibility in algebras of real symmetric functions. To appear in Math. Nachr. http://www.cdam.lse.ac.uk/Reports/Files/cdam-2007-20.pdf Google Scholar
[15] Vaseršteın, L. N., The stable range of rings and the dimension of topological spaces. (Russian) Funkcional. Anal. i Priložen. 5(1971), no. 2, 17–27. English translation in Functional Anal. Appl. 5(1971), 102–110.Google Scholar
[16] Vidyasagar, M., Control System Synthesis: A Factorization Approach. MIT Press Series in Signal Processing, Optimization, and Control 7. MIT Press, Cambridge, MA, 1985.Google Scholar
[17] Wick, B., A note about stabilization in ARD. Math. Nachr. 282(2009), no. 6, 912–916. doi:10.1002/mana.200610779 Google Scholar