Hostname: page-component-cd9895bd7-gvvz8 Total loading time: 0 Render date: 2024-12-24T16:41:01.506Z Has data issue: false hasContentIssue false
  • English
  • Français

Rectifiability of Optimal Transportation Plans

Published online by Cambridge University Press:  20 November 2018

Robert J. McCann ,
Brendan Pass  and
Micah Warren
Robert J. McCann
Affiliation:
Department of Mathematics, University of Toronto, Toronto, ON M5S 2E4 email: [email protected]
Brendan Pass
Affiliation:
Department of Mathematics, University of Toronto, Toronto, ON M5S 2E4, Current address: Department ofMathematical and Statistical Sciences, University of Alberta, Edmonton, AB T6G 2G1 email: [email protected]@ualberta.ca
Micah Warren
Affiliation:
Department of Mathematics, Princeton University, Princeton, NJ, USA 08544 email: [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

The regularity of solutions to optimal transportation problems has become a hot topic in current research. It is well known by now that the optimal measure may not be concentrated on the graph of a continuous mapping unless both the transportation cost and the masses transported satisfy very restrictive hypotheses (including sign conditions on the mixed fourth-order derivatives of the cost function). 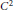The purpose of this note is to show that in spite of this, the optimal measure is supported on a Lipschitz manifold, provided only that the cost is ${{C}^{2}}$ with non-singular mixed second derivative. We use this result to provide a simple proof that solutions to Monge's optimal transportation problem satisfy a change of variables equation almost everywhere.

Keywords

49K2049K6035J9658C07
Type
Research Article
Information
Canadian Journal of Mathematics , Volume 64 , Issue 4 , 01 August 2012 , pp. 924 - 934
Copyright
Copyright © Canadian Mathematical Society 2012

References

[1] Adler, R. J., The geometry of random fields. Wiley Series in Probability and Mathematical Statistics, John Wiley and Sons, Ltd., Chichester, 1981.Google Scholar
[2] Agueh, M., Existence of solutions to degenerate parabolic equation via the Monge-Kantorovich theory. Ph D Dissertation, Georgia Institute of Technology, 2002.Google Scholar
[3] Ahmad, N., Kim, H.-K., and Mc Cann, R. J., Optimal transportation, topology and uniqueness. Bull. Math. Sci. 1(2011), no. 1, 13–32. http://dx.doi.org/10.1007/s13373-011-0002-7 Google Scholar
[4] Alberti, G. and Ambrosio, L., A geometrical approach to monotone functions on Rn. Math. Z. 230(1999), no. 2, 259–316. http://dx.doi.org/10.1007/PL00004691 Google Scholar
[5] Ambrosio, L., Fusco, N., and Pallara, D., Functions of bounded variation and free discontinuity problems. Oxford Mathematical Monographs, The Clarendon Press, Oxford University Press, New York, 2000.Google Scholar
[6] Ambrosio, L., Gigli, N., and Savaré, G., Gradient flows in metric spaces and in the space of probability measures. Lectures in Mathematics ETH Z’urich, Birkhäuser Verlag, Basel, 2005.Google Scholar
[7] Ambrosio, L. and Pratelli, A., Existence and stability results in the L 1-theory of optimal transportation. In: Optimal transportation and applications (Martina Franca, 2001), Lecture notes in Mathematics, 1813, Springer, Berlin, 2003, pp. 123–160.Google Scholar
[8] Beněs, V. and Štěpàn, J., The support of extremal probability measures with given marginals. In: Mathematical statistics and probability theory, A (Bad Tatzmannsdorf, 1986), Reidel, Dordrecht, 1987, pp. 33–41.Google Scholar
[9] Brenier, Y., Decomposition polaire et rearrangement monotone des champs de vecteurs. C. R. Acad. Sci. Pair. Ser. I Math. 305(1987), no. 19, 805–808.Google Scholar
[10] Caffarelli, L. A., The regularity of mappings with a convex potential. J. Amer. Math. Soc. 5(1992), no. 1, 99–104. http://dx.doi.org/10.1090/S0894-0347-1992-1124980-8 Google Scholar
[11] Caffarelli, L. A., Boundary regularity of maps with convex potentials. Comm. Pure Appl. Math. 45(1992), no. 9, 1141–1151. http://dx.doi.org/10.1002/cpa.3160450905 Google Scholar
[12] Caffarelli, L. A., Boundary regularity of maps with convex potentials. II. Ann. of Math. (2) 144(1996), no. 3, 453–496. http://dx.doi.org/10.2307/2118564 Google Scholar
[13] Cordero-Erausquin, D., Non-smooth differential properties of optimal transport. In: Recent advances in the theory and application of mass transport, Contemp. Math., 353, Amer. Math. Soc., Providence, RI, 2004, pp. 61–71.Google Scholar
[14] Cordero-Erausquin, D., Mc Cann, R. J., and Schmuckenschläger, M. A., Riemannian interpolation inequality à la Borell, Brascamp and Lieb. Invent. Math. 146(2001), no. 2, 219–257. http://dx.doi.org/10.1007/s002220100160 Google Scholar
[15] Delanöe, P., Classical solvability in dimension two of the second boundary-value problem associated with the Monge-Ampère operator. Ann. Inst. H. Poincaré Anal. Non Linéaire 8(1991), no. 5, 442–457.Google Scholar
[16] Delanöe, P., Gradient rearrangment for diffeomorphisms of a compact manifold. Differential Geom. Appl. 20(2004), no. 2, 145–165. http://dx.doi.org/10.1016/j.difgeo.2003.10.003 Google Scholar
[17] Douglas, R. G., On extremal measures and subspace density. Michigan Math. J. 11(1964), 243–246. http://dx.doi.org/10.1307/mmj/1028999137 Google Scholar
[18] Figalli, A. and Gigli, N., Local semiconvexity of Kantorovich potentials on non-compact manifolds. ESAIM Control Optim. Calc. Var., to appear.Google Scholar
[19] Figalli, A., Kim, Y.-H., and Mc Cann, R. J., Hölder continuity and injectivity of optimal maps. arxiv:1107.1014Google Scholar
[20] Gangbo, W., Habilitation thesis., Université de Metz, 1995.Google Scholar
[21] Gangbo, W. and Mc Cann, R. J., The geometry of optimal transportation. Acta Math. 177(1996), no. 2, 113–161. http://dx.doi.org/10.1007/BF02392620 Google Scholar
[22] Gigli, N., On the inverse implication of Brenier-Mc Cann theorems and the structure of (P2(M), W2). http://cvgmt.sns.it/media/doc/paper/983/Inverse.pdf Google Scholar
[23] Harvey, F. R. and Lawson, H. B., Jr, Split special Lagrangian geometry. arxiv:1007.0450v1Google Scholar
[24] Hestir, K. and Williams, S. C., Supports of doubly stochastic measures. Bernoulli 1(1995), no. 3, 217–243. http://dx.doi.org/10.2307/3318478 Google Scholar
[25] Kim, Y.-H., Mc Cann, R. J., and M.Warren, Pseudo-Riemannian geometry calibrates optimal transportation. Math. Res. Lett. 17(2010), no. 6, 1183–1197.Google Scholar
[26] Levin, V., Abstract cyclical monotonicity and Monge solutions for the general Monge-Kantorovich problem. Set-Valued Anal. 7(1999), no. 1, 7–32. http://dx.doi.org/10.1023/A:1008753021652 Google Scholar
[27] Lindenstrauss, J., A remark on extreme doubly stochastic measures. Amer. Math. Monthly 72(1965), 379–382. http://dx.doi.org/10.2307/2313497 Google Scholar
[28] Liu, J., Hölder regularity in optimal mappings in optimal transportation. Calc. Var. Partial Differential Equations 34(2009), no. 4, 435–451. http://dx.doi.org/10.1007/s00526-008-0190-5 Google Scholar
[29] Loeper, G., On the regularity of solutions of optimal transportation problems. Acta Math. 202(2009), no. 2, 241–283. http://dx.doi.org/10.1007/s11511-009-0037-8 Google Scholar
[30] Mc Afee, R. P. and Mc Millan, J., Multidimensional incentive compatibility and mechanism design. J. Econom. Theory 46(1988), no. 2, 335–354. http://dx.doi.org/10.1016/0022-0531(88)90135-4 Google Scholar
[31] Ma, X.-N., Trudinger, N., and Wang, X.-J., Regularity of potential functions of the optimal transportation problem. Arch. Ration. Mech. Anal. 177(2005), no. 2, 151–183. http://dx.doi.org/10.1007/s00205-005-0362-9 Google Scholar
[32] Mc Cann, R. J., Existence and uniqueness of monotone measure-preserving maps. Duke Math. J. 80(1995), no. 2, 309–323. http://dx.doi.org/10.1215/S0012-7094-95-08013-2 Google Scholar
[33] Mc Cann, R. J., A convexity principle for interacting gases. Adv. Math. 128(1997), no. 1, 153–179. http://dx.doi.org/10.1006/aima.1997.1634 Google Scholar
[34] Mc Cann, R. J., Exact solutions to the transportation problem on the line. R. Soc. Lond. Proc. Ser. A Math. Phys. Eng. Sci. 455(1999), no. 1984, 1341–1380. http://dx.doi.org/10.1098/rspa.1999.0364 Google Scholar
[35] Minty, G. J., Monotone (nonlinear) operators in Hilbert space. Duke Math. J. 29(1962), 341–346. http://dx.doi.org/10.1215/S0012-7094-62-02933-2 Google Scholar
[36] Mirrlees, J. A., An exploration in the theory of optimum income taxation. Rev. Econom. Stud. 38(1971), no. 2, 175–208.Google Scholar
[37] Smith, C. and Knott, M., On Hoeffding-Fréchet bounds and cyclic monotone relations. J. Multivariate Anal. 40(1992), no. 2, 328–334. http://dx.doi.org/10.1016/0047-259X(92)90029-F Google Scholar
[38] Spence, M., Competitive and optimal responses to signals: An analysis of efficiency and distribution. J. Econom. Theory 7(1974), no. 3, 296–332.Google Scholar
[39] Trudinger, N., and Wang, X.-J., On the second boundary value problem for Monge-Ampère type equations and optimal transportation. Ann. Sc. Norm. Super. Pisa Cl. Sci. 8(2009), no. 1, 143–174.Google Scholar
[40] Urbas, J., On the second boundary value problem for equations of Monge-Ampère type. J. Reine Angew. Math. 487(1997), 115–124. http://dx.doi.org/10.1515/crll.1997.487.115 Google Scholar
[41] Villani, C., Optimal transport: Old and new. Grundlehren der Mathematischen Wissenschaften, 338, Springer-Verlag, Berlin, 2009.Google Scholar
[42] Wang, X.-J., On the design of a reflector antenna. Inverse Problems 12(1996), no. 3, 351–375. http://dx.doi.org/10.1088/0266-5611/12/3/013Google Scholar