Hostname: page-component-cd9895bd7-jn8rn Total loading time: 0 Render date: 2024-12-25T15:48:59.188Z Has data issue: false hasContentIssue false
  • English
  • Français

Rational Interpolation of the Exponential Function

Published online by Cambridge University Press:  20 November 2018

L. Baratchart ,
E. B. Saff  and
F. Wielonsky
L. Baratchart
Affiliation:
INRIA 2004, Route des Lucioles B.P. 93 06902 Sophia Antipolis Cedex France e-mail: [email protected]
E. B. Saff
Affiliation:
Department of Mathematics University of South Florida Tampa, Florida 33620 U.S.A. e-mail: [email protected]
F. Wielonsky
Affiliation:
INRIA 2004, Route des Lucioles B.P. 93 06902 Sophia Antipolis Cedex France e-mail: [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

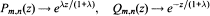Let m, n be nonnegative integers and B(m+n) be a set of m + n + 1 real interpolation points (not necessarily distinct). Let Rm,n = Pm,n/Qm.n be the unique rational function with deg Pm,n ≤ m, deg Qm,n ≤ n, that interpolates ex in the points of B(m+n). If m = mv, n = nv with mv + nv → ∞, and mv / nv → λ as v → ∞, and the sets B(m+n) are uniformly bounded, we show that locally uniformly in the complex plane C, where the normalization Qm,n(0) = 1 has been imposed. Moreover, for any compact set K ⊂ C we obtain sharp estimates for the error |ez — Rm,n(z)| when z ∈ K. These results generalize properties of the classical Padé approximants. Our convergence theorems also apply to best (real) Lp rational approximants to ex on a finite real interval.

Keywords

41A0541A21
Type
Research Article
Information
Canadian Journal of Mathematics , Volume 47 , Issue 6 , 01 December 1995 , pp. 1121 - 1147
Copyright
Copyright © Canadian Mathematical Society 1995

References

1. Arms, R.J. and Edrei, A., The Padé tables and continued fractions generated by totally positive sequences. In: Mathematical Essays dedicated to A.J.Macintyre, Ohio Univ. Press, Athens, Ohio, 1970. 1—21.Google Scholar
2. Baker, G.A., Jr., Essentials of Padé Approximants, Academic Press, New York, 1975.Google Scholar
3. Blatt, H.P., Saffand, E.B. Simkani, M., Jentzsch-Szegő type theorems for the zeros of best approximants,, J. London Math. Soc. 38(1988), 307–316.Google Scholar
4. Borwein, P.B., Rational interpolation to ex, J. Approx. Theory 35(1982), 142–147.Google Scholar
5. Borwein, P.B., Rational interpolation to ex, II, SIAM.J.Math. Anal. (3) 16(1985), 656–662.Google Scholar
6. Braess, D., Nonlinear Approximation Theory, Springer Ser. Comp. Math. 7, Springer Verlag, Berlin, 1986.Google Scholar
7. Cheney, E.W. and Goldstein, A.A., Mean-square approximation by generalized rational functions,, Math. Z. 95(1967), 232–241.Google Scholar
8. Hermite, C., Sur la fonction exponentielle, C.R. Acad. Sci. Paris 77(1873), 18–24. 74-79, 226–233. 285-293.Google Scholar
9. Iserles, A. and Powell, M.J.D., On the A-acceptability of rational approximations that interpolate the exponential function, IMA J. Numer. Anal. 1(1981), 241–251.Google Scholar
10. Jackson, D., Theory of Approximation, Amer. Math. Soc. Colloq. Publ. XI, Providence, Rhode Island, 1930.Google Scholar
11. Marden, M., Geometry of Polynomials, Math. Surveys 3, Amer. Math. Soc, Providence, Rhode Island, 1966.Google Scholar
12. Padé, H., Mémoire sur les développements en fractions continues de la fonction exponentielle pouvant servir d'introduction à la théorie des fractions continues algébriques, Ann. Sci. École Norm. Sup. (3) 16(1899), 395–426.Google Scholar
13. Padé, H., Sur la représentation approchée d'une fonction par des fractions rationelles, Ann. Sci. Ecole Norm. Sup. (3) 9(1892), Supplément, 3–93.Google Scholar
14. Padé, H., Oeuvres, Brezinski, C., éd., Librairie Scientifique et Technique, A. Blanchard, Paris, 1984.Google Scholar
15. Perron, O., Die Lehre von den Kettenbrùchen, 3rd Edition, Teubner 2, Stuttgart, 1957.Google Scholar
16. Rivlin, T.J., An Introduction to the Approximation of Functions, Dover, New York, 1969.Google Scholar
17. Saff, E.B., Orthogonal polynomials from a complex perspective. In: Orthogonal Polynomials, (ed. Nevai, P.), Kluwer Academic, 1990. 363–393,Google Scholar
18. Saffand, E.B. Varga, R.S., On the zeros and poles of Padé approximants to ez, Numer. Math. 25(1975), 1–14.Google Scholar
19. Saffand, E.B., Zero-free parabolic regions for sequences of polynomials, SIAM J. Math. Anal. 7(1976), 344–357.Google Scholar
20. Saffand, E.B., On the zeros and poles of Padé approximants to ez, III, Numer. Math. 30(1978), 241–266.Google Scholar
21. Siegel, C.L., Transcendental Numbers, Princeton Univ. Press, Princeton, 1949.Google Scholar
22. Tsuji, M., Potential Theory in Modern Function Theory, Maruzen, Tokyo, 1959.Google Scholar
23. Wanner, G., Hairer, E. and Nørsett, S.P., Order stars and stability theorems, BIT 18(1978), 475–489.Google Scholar