Hostname: page-component-cd9895bd7-lnqnp Total loading time: 0 Render date: 2024-12-26T00:32:18.186Z Has data issue: false hasContentIssue false
  • English
  • Français

Rational Equivalence of Fibrations with Fibre G/K

Published online by Cambridge University Press:  20 November 2018

Stephen Halperin  and
Jean Claude Thomas
Stephen Halperin
Affiliation:
University of Toronto, Toronto y Ontario
Jean Claude Thomas
Affiliation:
Université de Lille I, Villeneuve D'Ascq, France
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let 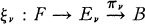be two Serre fibrations with same base and fibre in which all the spaces have the homotopy type of simple CW complexes of finite type. We say they are rationally homotopically equivalent if there is a homotopy equivalence 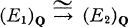between the localizations at Q which covers the identity map of BQ.

Such an equivalence implies, of course, an isomorphism of cohomology algebras (over Q) and of rational homotopy groups; on the other hand isomorphisms of these classical algebraic invariants are usually (by far) insufficient to establish the existence of a rational homotopy equivalence.

Nonetheless, as we shall show in this note, for certain fibrations rational homotopy equivalence is in fact implied by the existence of an isomorphism of cohomology algebras. While these fibrations are rare inside the class of all fibrations, they do include principal bundles with structure groups a connected Lie group G as well as many associated bundles with fibre G/K.

Type
Research Article
Information
Canadian Journal of Mathematics , Volume 34 , Issue 1 , 01 February 1982 , pp. 31 - 43
Copyright
Copyright © Canadian Mathematical Society 1982

References

1. Borel, A., Sur la cohomologie des espaces fibres principaux et des espaces homogènes de groupes de Lie compacts, Ann. of Math. 57 (1953), 115–207.Google Scholar
2. Cartan, H., La transgression dans un groupe de Lie, Colloque de Topologie (espaces fibres) Masson, Paris (1951), 51–71.Google Scholar
3. Greub, W. et al., Connections, curvature and cohomology III (Academic Press, New York, 1976).Google Scholar
4. Halperin, S., Finiteness in the minimal models of Sullivan, Trans. Amer. Math. Soc. 230 (1977), 173–199.Google Scholar
5. Halperin, S., Lectures on minimal models, Publ. Internes de l'U.E.R. de Mathématiques Pures, Université de Lille I, 59650 Villeneuve d'Asq.Google Scholar
6. Halperin, S. and Stashefï, J. D., Obstructions to homotopy equivalences, Advances in Mathematics 32 (1979), 233–279.Google Scholar
7. Halperin, S., Rational fibrations, minimal models, and fibrings of homogeneous spaces, Trans. Amer. Math. Soc. 2U (1978), 199–224.Google Scholar
8. Sullivan, D., Infinitesimal computations in topology, Publ. de l'Institut des Hautes Etudes Scientifiques 47 (1977), 269–331.Google Scholar
9. Thomas, J. C., Homotopie rationnelle des fibres de Serre, Thèse n° 473, Université de Lille I.Google Scholar