Hostname: page-component-cd9895bd7-fscjk Total loading time: 0 Render date: 2024-12-26T00:42:34.130Z Has data issue: false hasContentIssue false
  • English
  • Français

Rational Approximation to xn II

Published online by Cambridge University Press:  20 November 2018

D. J. Newman  and
A. R. Reddy
D. J. Newman
Affiliation:
Temple University, Philadelphia, Pennsylvania
A. R. Reddy
Affiliation:
University of Hyderabad, Hyderabad, India
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Introduction. In 1858 Chebyshev showed that xn+l can be approximated uniformly on [–1, 1] by polynomials of degree at most n with an error 2–n. Let 0 ≦ σ ≦ (n + l)tan2(π/2n + 2). In 1868 Zolotarev established that x n + 1σxn can be approximated uniformly on [ –1, 1] by polynomials of degree at most (n – 1) with an error 2–n(l + σ/n + l)n+1. It is interesting to note that for the case σ = 0, Zolotarev's result includes Chebyshev's result. Achieser ([1], p. 279) proved the following analogue for rational approximation. Let a0 ≠ 0, a1, a2, a3, …, an be any given real numbers. Then for every N > n,

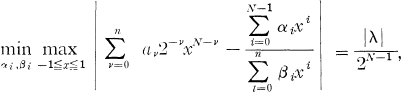
where λ is numerically the smallest root of the polynomial

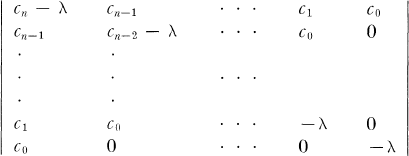
with

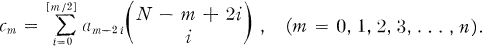
Type
Research Article
Information
Canadian Journal of Mathematics , Volume 32 , Issue 2 , February 1980 , pp. 310 - 316
Copyright
Copyright © Canadian Mathematical Society 1980

References

1. Achieser, N. I., Theory of approximation (Frederick Ungar Publishing Co., New York, 1956).Google Scholar
2. Newman, D. J., Rational approximation to xn, J. Approximation Theor. 22 (1978), 285–288.Google Scholar
3. Newman, D. J. and Reddy, A. R., Rational approximation to xn, Pacific J. Mathematic. 67 (1976), 247–250.Google Scholar
4. Timan, A. F., Theory of approximation of functions of a real variable, International series of monographs in pure and applied mathematics 34 (Macmillan, New York, 1963).Google Scholar
5. Voronovskaja, E. V., The functional method and its applications (English translation), American Math. Society, Providence, RI (1970).Google Scholar