Hostname: page-component-586b7cd67f-rdxmf Total loading time: 0 Render date: 2024-11-26T00:58:15.126Z Has data issue: false hasContentIssue false
  • English
  • Français

Ratio and Stochastic Ergodic Theorems for Superadditive Processes

Published online by Cambridge University Press:  20 November 2018

Humphrey Fong
Humphrey Fong*
Affiliation:
Bowling Green State University, Bowling Green, Ohio
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

1. Introduction. Let (X, 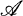, m) be a σ-finite measure space and let T be a positive linear operator on L1 = L1(X, 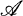, m). T is called Markovian if

(1.1)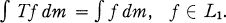

T is called sub-Markovian if

(1.2)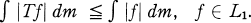

All sets and functions are assumed measurable; all relations and statements are assumed to hold modulo sets of measure zero.

For a sequence of L1+ functions (ƒ0, ƒ1, ƒ2, …), let

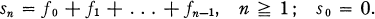
(ƒn) is called a super additive sequence or process, and (sn) a super additive sum relative to a positive linear operator T on L1 if

(1.3)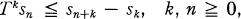

and

(1.4)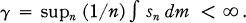

Type
Research Article
Information
Canadian Journal of Mathematics , Volume 31 , Issue 2 , 01 April 1979 , pp. 441 - 447
Copyright
Copyright © Canadian Mathematical Society 1979

References

1. Akcoglu, M. A. and Sucheston, L., A ratio ergodic theorem for super-additive processes, preprint. For a resume, see C. R. Acad. Sci., Paris. 285 (1977), 637 639.Google Scholar
2. Chacon, R. V., Convergence of operator averages, in Ergodic theory (Academic Press, New-York, 1963, 89 120.Google Scholar
3. Chacon, R. V., A class of linear transformations, Proc. Amer. Math. Soc. 15 (1964), 560 564.Google Scholar
4. Chacon, R. V. and Ornstein, D. S., A general ergodic theorem, Illinois J. Math. 4 (1960), 153 160.Google Scholar
5. Derriennic, Y., Sur le theorem ergodique sous-additif, C. R. Acad. Sci., Paris. 281 (1975), 985 988.Google Scholar
6. Derriennic, Y. and Lin, M., On invariant measures and ergodic theorems for positive operators, J. Functional Anal. 13 (1973), 252 267.Google Scholar
7. Fong, H., On invariant functions for positive operators, Colloq. Math. 22 (1970), 75 84.Google Scholar
8. Ionescu-Tulcea, A. and Moretz, M., Ergodic properties of semi-Markovian operators on the Z-part, Z. Wahrscheinlichkeitstheorie verw. Geb. 13 (1969), 119 122.Google Scholar
9. Kingman, J. F. C., The ergodic theory of subadditive stochastic processes, J. Royal Statist. Soc.. 30 (1968), 499 510.Google Scholar
10. Kingman, J. F. C., Subadditive ergodic theory, Ann. Prob. 1 (1973), 883 905.Google Scholar
11. Kingman, J. F. C., Subadditive processes, Ecole d't des probabilits de Saint-Flour, Springer Verlag Lecture Notes in Mathematics, Vol. 539 (1976), 168 223.Google Scholar
12. Krengel, U., On the global limit behaviour of Markov chains and of general nonsingular Markov processes, Z. Wahrscheinlichkeitstheorie verw. Geb. 6 (1966), 302 316.Google Scholar
13. Sucheston, L., On the ergodic theorem for positive operators, I, Z. Wahrscheinlichkeitstheorie verw. Geb. 8 (1967), 1 11.Google Scholar