Hostname: page-component-586b7cd67f-t7czq Total loading time: 0 Render date: 2024-11-26T17:19:21.248Z Has data issue: false hasContentIssue false
  • English
  • Français

Rankings and Ranking Functions

Published online by Cambridge University Press:  20 November 2018

W. J. Walker
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Suppose that n competitors compete in r races and in each race they are awarded placings l, 2, 3, …, n – 1, n. After the r races each competitor has a result consisting of his r placings. Let such a result be written (αj)1≦j≦r where for convenience the positive integers αj are arranged in ascending order. For example, if n = 4 and r = 6 a typical result is (1, 2, 2, 3, 4, 4).

A final ranking of the n competitors will be determined in all circumstances if a strict ordering is assigned to all possible results. In the next section it is shown that the number or results is 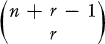. Of course only some strict orderings of this set of results will be feasible in that there are criteria which a final ranking should satisfy. For example, (1, 1, …, 1) should clearly be ranked first in any feasible ranking.

Type
Research Article
Information
Canadian Journal of Mathematics , Volume 33 , Issue 2 , 01 April 1981 , pp. 395 - 399
Copyright
Copyright © Canadian Mathematical Society 1981

References

1. Brualdi, R. A., Introductory combinatorics (North Holland, New York, 1977).Google Scholar
2. Fan, K., Systems of linear inequalities, in: Linear inequalities and related systems (Princeton Univ. Press, Princeton, N.J., 1956).Google Scholar
3. Hardy, G. H. and Wright, E. M., An introduction to the theory of numbers (Oxford Press, 1938).Google Scholar
4. Walker, W. J., Algebraic and combinatorial results for ranking competitors in a sequence of races, Discrete Math. U (1976), 297–304.Google Scholar
5. Walker, W. J., The enumeration and bifurcations of ranking functions, Bull. Austral. Math. Soc. 18 (1978), 287–292.Google Scholar