Hostname: page-component-848d4c4894-sjtt6 Total loading time: 0 Render date: 2024-06-25T05:38:35.807Z Has data issue: false hasContentIssue false
  • English
  • Français

Rank conditions for finite group actions on 4-manifolds

Part of: Topological manifolds

Published online by Cambridge University Press:  18 January 2021

Ian Hambleton  and
Semra Pamuk
Ian Hambleton*
Affiliation:
McMaster University, Hamilton, ON, Canada
Semra Pamuk
Affiliation:
Middle East Technical University, Ankara, Turkey e-mail: [email protected]
*
e-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

Let M be a closed, connected, orientable topological 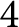$4$ -manifold, and G be a finite group acting topologically and locally linearly on M. In this paper, we investigate the spectral sequence for the Borel cohomology 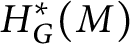$H^*_G(M)$ and establish new bounds on the rank of G for homologically trivial actions with discrete singular set.

Keywords

finite group actions4-manifoldsBorel spectral sequence

MSC classification

Primary: 57S17: Finite transformation groups
Secondary: 57S25: Groups acting on specific manifolds 57N65: Algebraic topology of manifolds
Type
Article
Information
Canadian Journal of Mathematics , Volume 74 , Issue 2 , April 2022 , pp. 550 - 572
Check for updates
Copyright
© Canadian Mathematical Society 2021

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

This project was partially supported by NSERC Discovery Grant A4000. The first author wishes to thank the Max Planck Institut für Mathematik for its hospitality and support in November 2019. The second author was supported on sabbatical by METU and thanks McMaster University for its hospitality during the academic year 2018–19.

References

Altunbulak Aksu, F. and Green, D. J., Essential cohomology for elementary abelian p-groups . J. Pure Appl. Algebra 213(2009), 2238–2243.10.1016/j.jpaa.2009.04.016CrossRefGoogle Scholar
Borel, A., Seminar on transformation groups. In: With contributions by Bredon, G., Floyd, E. E., Montgomery, D., Palais, R., Annals of Mathematics Studies, 46, Princeton University Press, Princeton, NJ, 1960.Google Scholar
Breton, S., Finite group actions on the four-dimensional sphere. Master’s thesis, McMaster University, 2011.Google Scholar
Edmonds, A. L., Aspects of group actions on four-manifolds . Topology Appl. 31(1989), 109–124.10.1016/0166-8641(89)90075-8CrossRefGoogle Scholar
Edmonds, A. L., Homologically trivial group actions on 4-manifolds. Preprint, 1998. arxiv:math/9809055v1 Google Scholar
Hambleton, I. and Kreck, M., On the classification of topological 4-manifolds with finite fundamental group . Math. Ann. 280(1988), 85–104.10.1007/BF01474183CrossRefGoogle Scholar
Hambleton, I. and Kreck, M., Cancellation, elliptic surfaces and the topology of certain four-manifolds . J. Reine Angew. Math. 444(1993), 79–100.Google Scholar
Hambleton, I. and Kreck, M., Cancellation of hyperbolic forms and topological four-manifolds . J. Reine Angew. Math. 443(1993), 21–47.Google Scholar
Hambleton, I., Kreck, M., and Teichner, P., Nonorientable 4-manifolds with fundamental group of order 2. Trans. Amer. Math. Soc. 344(1994), 649–665.Google Scholar
Hambleton, I. and Lee, R., Smooth group actions on definite 4-manifolds and moduli spaces . Duke Math. J. 78(1995), 715–732.10.1215/S0012-7094-95-07826-0CrossRefGoogle Scholar
Hausmann, J.-C. and Weinberger, S., Caractéristiques d’Euler et groupes fondamentaux des variétés de dimension 4. Comment. Math. Helv. 60(1985), 139–144.10.1007/BF02567405CrossRefGoogle Scholar
Kirk, P. and Livingston, C., The geography problem for 4-manifolds with specified fundamental group . Trans. Amer. Math. Soc. 361(2009), 4091–4124.10.1090/S0002-9947-09-04649-2CrossRefGoogle Scholar
Mann, L. N. and Su, J. C., Actions of elementary p-groups on manifolds . Trans. Amer. Math. Soc. 106(1963), 115–126.Google Scholar
McCooey, M. P., Symmetry groups of four-manifolds . Topology 41(2002), 835–851.10.1016/S0040-9383(01)00006-4CrossRefGoogle Scholar
McCooey, M. P., Groups that act pseudofreely on S 2 × S 2 . Pacific J. Math. 230(2007), 381–408.10.2140/pjm.2007.230.381CrossRefGoogle Scholar
McCooey, M. P., Symmetry groups of non-simply-connected four-manifolds. Preprint, 2013. arxiv:0707.3835v2 [math.GT]Google Scholar
Ono, K., On a theorem of Edmonds. In: Progress in differential geometry, Adv. Stud. Pure Math., 22, Mathematical Society of Japan, Tokyo, 1993, pp. 243–245.Google Scholar
Sikora, A. S., Torus and ℤ/p actions on manifolds . Topology 43(2004), 725–748.10.1016/j.top.2003.10.009CrossRefGoogle Scholar
Smith, P. A., New results and old problems in finite transformation groups . Bull. Amer. Math. Soc. 66(1960), 401–415.10.1090/S0002-9904-1960-10491-0CrossRefGoogle Scholar
tom Dieck, T., Transformation groups. de Gruyter Studies in Mathematics, 8, Walter de Gruyter, Berlin, 1987.10.1515/9783110858372CrossRefGoogle Scholar