Hostname: page-component-cd9895bd7-dk4vv Total loading time: 0 Render date: 2024-12-24T14:15:38.666Z Has data issue: false hasContentIssue false
  • English
  • Français

The Ramsey Property for Families of Graphs Which Exclude a Given Graph

Published online by Cambridge University Press:  20 November 2018

V. Rödl  and
N. Sauer
V. Rödl
Affiliation:
Emory University, Atlanta, Georgia, U.S.A.
N. Sauer
Affiliation:
University of Calgary, Calgary, Alberta
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

For graphs A, B and a positive integer r, the relation 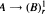means that whenever Δ is an r-colouring of the vertices of A, then there is an embedding ϕ of B into A such that Δ ∘ ϕ is constant. A class of graphs 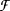has the Ramsey property if, for every 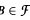, there is an 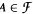such that 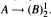. For a given finite graph G, let Forb(G) denote the class of all finite graphs which do not embed G. It is known that, if G is 2-connected, then Forb(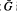) has the Ramsey property, and Forb(G) has the Ramsey property if and only if Forb(G) also has the Ramsey property. In this paper we show that if neither G nor its complement 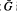is 2-connected, then either (i) G has a cut point adjacent to every other vertex, or (ii) G has a cut point adjacent to every other vertex except one. We show that Forb(G) has the Ramsey property if G is a path of length 2 or 3, but that Forb(G) does not have the Ramsey property if (i) holds and G is not the path of length 2.

Keywords

05B
Type
Research Article
Information
Canadian Journal of Mathematics , Volume 44 , Issue 5 , 01 October 1992 , pp. 1050 - 1060
Copyright
Copyright © Canadian Mathematical Society 1992

References

1. Erdős, R. and Hajnal, A., On chromatic number of graphs and set systems, Acta. Math. Acad. Sci. Hung. 17(1966), 61–99.Google Scholar
2. NeSetfil, J. and Rödl, V., Partitions of vertices, Comment. Math. Univ. Carolina 17(1976), 85–95.Google Scholar
3. Nešetřil, J. and Rödl, V., Partitions of finite relational and set systems, J. Combin. Theory (A) 22, 289–312.Google Scholar
4. Sauer, N. and Zhu, X., Graphs which do not embed a given graph and the Ramsey property, manuscript.Google Scholar