Throughout, we consider a finite Galois extension L|K of non-archimedian valued fields which are maximally complete [2, Chapter 2], Let v denote the valuation on L and let L* denote the group of non-zero elements of L. We mayidentify the value group v(L*) of L with a subgroup of D, where D denotes the minimal divisible ordered group containing v(K*). We denote the residue field of L by 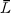, and will always assume that the field extension 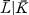is separable. The characteristic of 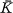will invariably be denoted by p ; much of what follows is trivial in case p = 0.