Hostname: page-component-78c5997874-8bhkd Total loading time: 0 Render date: 2024-11-16T17:21:39.176Z Has data issue: false hasContentIssue false
  • English
  • Français

Ramification of the Eigencurve at Classical RM Points

Part of: Algebraic number theory: global fields Discontinuous groups and automorphic forms

Published online by Cambridge University Press:  07 March 2019

Adel Betina
Adel Betina*
Affiliation:
School of Mathematics and Statistics, The University of Sheffield, Sheffield S3 7RH, UK Email: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

J. Bellaïche and M. Dimitrov showed that the 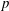$p$-adic eigencurve is smooth but not étale over the weight space at 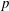$p$-regular theta series attached to a character of a real quadratic field 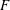$F$ in which 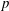$p$ splits. In this paper we prove the existence of an isomorphism between the subring fixed by the Atkin–Lehner involution of the completed local ring of the eigencurve at these points and a universal ring representing a pseudo-deformation problem. Additionally, we give a precise criterion for which the ramification index is exactly 2. We finish this paper by proving the smoothness of the nearly ordinary and ordinary Hecke algebras for Hilbert modular forms over 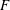$F$ at the overconvergent cuspidal Eisenstein points, being the base change lift for 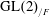$\text{GL}(2)_{/F}$ of these theta series. Our approach uses deformations and pseudo-deformations of reducible Galois representations.

Keywords

weight one RM modular formeigencurvepseudo-deformationdeformation of reducible representation

MSC classification

Primary: 11F80: Galois representations
Secondary: 11F33: Congruences for modular and $p$-adic modular forms 11R23: Iwasawa theory
Type
Article
Information
Canadian Journal of Mathematics , Volume 72 , Issue 1 , February 2020 , pp. 57 - 88
Copyright
© Canadian Mathematical Society 2019 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

The author’s research was supported by the EPSRC Grant EP/R006563/1. The author also received funding from the European Research Council (ERC) under the European Union’s Horizon 2020 research and innovation programme (grant agreement No 682152).

References

Andreatta, F., Iovita, A., and Pilloni, V., On overconvergent Hilbert modular cusp forms . Astérisque 382(2016), 163–193.Google Scholar
Bellaïche, J. and Chenevier, G., Lissité de la courbe de Hecke de GL(2) aux points Eisenstein critiques . J. Inst. Math. Jussieu 5(2006), 333–349. https://doi.org/10.1017/S1474748006000028.Google Scholar
Bellaïche, J. and Dimitrov, M., On the eigencurve at classical weight 1 points . Duke Math. J. 165(2016), no. 2, 245–266. https://doi.org/10.1215/00127094-3165755.Google Scholar
Betina, A., Les Variétés de Hecke-Hilbert aux points classiques de poids un . J. Théor. Nombres Bordeaux, to appear.Google Scholar
Bijakowski, S., Classicité de formes modulaires de Hilbert . Asterisque 382(2016), 49–71.Google Scholar
Buzzard, K., Eigenvarieties . In: L-functions and Galois representations . London Math. Soc. Lecture Note Ser., 320. Cambridge Univ. Press, Cambridge, 2007, pp. 59–120. https://doi.org/10.1017/CBO9780511721267.004.Google Scholar
Chenevier, G., Familles p-adiques de formes automorphes pour GLn . J. Reine Angew. Math. 570(2004), 143–217. https://doi.org/10.1515/crll.2004.031.Google Scholar
Cho, S., Deformations of induced Galois representations. Ph.D. thesis, University of California, Los Angeles, 1999.Google Scholar
Cho, S. and Vatsal, V., Deformations of induced Galois representations . J. Reine Angew. Math. 556(2003), 79–98. https://doi.org/10.1515/crll.2003.025.Google Scholar
Coleman, R., Classical and overconvergent modular forms . Invent. Math. 124(1996), 215–241. https://doi.org/10.1007/s002220050051.Google Scholar
Coleman, R. and Mazur, B., The eigencurve . In: Galois representations in arithmetic algebraic geometry . London Math. Soc. Lecture Note Ser., 254. Cambridge Univ. Press, Cambridge, 1998, pp. 1–113. https://doi.org/10.1017/CBO9780511662010.003.Google Scholar
Darmon, H., Lauder, A., and Rotger, V., Stark points and p-adic iterated integrals attached to modular forms of weight one . Forum Math. Pi 3(2015) . https://doi.org/10.1017/fmp.2015.7.Google Scholar
Darmon, H., Overconvergent generalised eigenforms of weight one and class fields of real quadratic fields . Adv. Math. 283(2015), 130–142. https://doi.org/10.1016/j.aim.2015.07.007.Google Scholar
Deligne, P. and Serre, J.-P., Formes modulaires de poids 1 . Ann. Sci. École Norm. Sup. (4), 7(1974), 507–530. https://doi.org/10.24033/asens.1277.Google Scholar
Deo, S., On the eigenvariety of Hilbert modular forms at classical parallel weight one points with dihedral projective image . Trans. Amer. Math. Soc. 370(2018), no. 6, 3885–3912. https://doi.org/10.1090/tran/7064.Google Scholar
Dimitrov, M., On the local structure of ordinary Hecke algebras at classical weight one points . In: Automorphic forms and Galois representations, vol. 2 . London Math. Soc. Lecture Note Series, 415. Cambridge Univ. Press, Cambridge, 2014, pp. 1–16.Google Scholar
Dimitrov, M. and Ghate, E., On classical weight one forms in Hida families . J. Théor. Nombres Bordeaux 24(2012), no. 3, 669–690. https://doi.org/10.5802/jtnb.816.Google Scholar
Doi, K., Hida, H., and Ishii, H., Discriminant of Hecke fields and twisted adjoint L-values for GL(2) . Invent. Math. 134(1998), no. 3, 547–577. https://doi.org/10.1007/s002220050273.Google Scholar
Gouvea, F., On the ordinary Hecke algebra . J. Number Theory 41(1992), no. 2, 178–198. https://doi.org/10.1016/0022-314X(92)90119-A.Google Scholar
Greenberg, R., The Iwasawa invariant of 𝛤-extensions of a fixed number field . Amer. J. Math. 95(1973), 204–214. https://doi.org/10.2307/2373652.Google Scholar
Hida, H., Galois representations into GL2 (ℤp [[X]]) attached to ordinary cusp forms . Invent. Math. 85(1986), no. 3, 545–613. https://doi.org/10.1007/BF01390329.Google Scholar
Hida, H., On nearly ordinary Hecke algebras for GL(2) over totally real fields . Adv. Stud. Pure Math. 17(1989), 139–169.Google Scholar
Hida, H., Nearly ordinary Hecke algebra and Galois representation of several variables . In: Algebraic analysis, geometry, and number theory . Johns Hopkins Univ. Press, Baltimoe, MD, 1989, pp. 115–134.Google Scholar
Hida, H., Global quadratic units and Hecke algebras . Doc. Math. 3(1998), 273–285.Google Scholar
Hida, H., On Selmer groups of adjoint modular Galois representations . In: Number theory . London Math. Soc Lecture Notes Ser., 235. Cambridge Univ. Press, Cambridge, 1996, pp. 89–132. https://doi.org/10.1017/CBO9780511662003.005.Google Scholar
Kisilevsky, H., Some non-semi-simple Iwasawa modules . Compositio Math. 49(1983), no. 3, 399–404.Google Scholar
Kisin, M., Overconvergent modular forms and the Fontaine-Mazur conjecture . Invent. Math. 153(2003), no. 2, 373–454. https://doi.org/10.1007/s00222-003-0293-8.Google Scholar
Langlands, R., Base change for GL2 . Annals of Mathematics Studies, 96. Princeton University Press, Princeton, NJ, 1980.Google Scholar
Nyssen, L., Pseudo-représentations . Math. Ann. 306(1996), 257–283. https://doi.org/10.1007/BF01445251.Google Scholar
Pilloni, V., Formes modulaires surconvergentes . Ann. Inst. Fourier (Grenoble) 63(2013), no. 1, 219–239. https://doi.org/10.5802/aif.2759.Google Scholar
Pilloni, V. and Stroh, B., Surconvergence et classicité: le cas Hilbert . J. Ramanujan Math. Soc. 32(2017), no. 4, 355–396.Google Scholar
Rouquier, R., Caractérisation des caractères et pseudo-caractères . J. Algebra 180(1996), 571–586. https://doi.org/10.1006/jabr.1996.0083.Google Scholar
Serre, J. P., Classes des corps cyclotomiques (d’après K. Iwasawa) . Séminaire Bourbaki, Vol. 5. Soc. Math., France, Paris, 1995, 174, 83–93.Google Scholar
Skinner, C. M. and Wiles, A., Residually reducible representations and modular forms . Inst. Hautes Études Sci. Publ. Math. (1999), no. 89, 5–126.Google Scholar
Taylor, R., Galois representations associated to Siegel modular forms of low weight . Duke Math. J. 63(1991), no. 2, 281–332. https://doi.org/10.1215/S0012-7094-91-06312-X.Google Scholar
Taylor, R. and Wiles, A., Ring theoretic properties of certain Hecke algebras . Ann. of Math. (2) 141(1995), no. 3, 553–572. https://doi.org/10.2307/2118560.Google Scholar
Wiles, A., On ordinary 𝜆-adic representations associated to modular forms . Invent. Math. 94(1988), no. 3, 529–573. https://doi.org/10.1007/BF01394275.Google Scholar
Wiles, A., Modular elliptic curves and Fermat’s last theorem . Ann. of Math. (2) 141(1995), no. 3, 443–551. https://doi.org/10.2307/2118559.Google Scholar