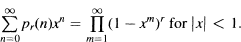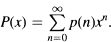Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Narkiewicz, Władysław
2012.
Rational Number Theory in the 20th Century.
p.
13.
Du, Julia Q. D.
Liu, Edward Y. S.
and
Zhao, Jack C. D.
2019.
Congruence properties of pk(n).
International Journal of Number Theory,
Vol. 15,
Issue. 06,
p.
1267.
van Hoeij, Mark
and
Radu, Cristian-Silviu
2021.
Transcendence in Algebra, Combinatorics, Geometry and Number Theory.
Vol. 373,
Issue. ,
p.
355.
Pascadi, Alexandru
2022.
Computer-assisted proofs of congruences for multipartitions and divisor function convolutions, based on methods of differential algebra.
The Ramanujan Journal,
Vol. 57,
Issue. 1,
p.
1.
Petta Mestrige, Shashika
2022.
Congruences for a class of eta-quotients and their applications.
The Ramanujan Journal,
Vol. 58,
Issue. 2,
p.
407.
Atmani, Sofiane
Bayad, Abdelmejid
and
Hernane, Mohand Ouamar
2023.
Congruences for Fourier coefficients of eta‐quotients modulo powers of 5, 7, 11, 13, and 17.
Mathematical Methods in the Applied Sciences,
Vol. 46,
Issue. 5,
p.
5001.
Du, Julia Q.D.
and
Tang, Dazhao
2024.
Congruences modulo powers of 5 for Ramanujan's ϕ function.
Journal of Mathematical Analysis and Applications,
Vol. 537,
Issue. 1,
p.
128260.