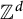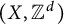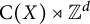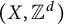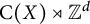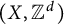1 Introduction
Let
![]() $(X, \Gamma )$
be a topological dynamical system, where X is a compact Hausdorff space and
$(X, \Gamma )$
be a topological dynamical system, where X is a compact Hausdorff space and
![]() $\Gamma $
is a discrete amenable group. The mean (topological) dimension of
$\Gamma $
is a discrete amenable group. The mean (topological) dimension of
![]() $(X, \Gamma )$
, denoted by
$(X, \Gamma )$
, denoted by
![]() $\mathrm {mdim}(X, \Gamma )$
, was introduced by Gromov [Reference Gromov11], and then was developed and studied systematically by Lindenstrauss and Weiss [Reference Lindenstrauss and Weiss26]. It is a numerical invariant, taking values in the range
$\mathrm {mdim}(X, \Gamma )$
, was introduced by Gromov [Reference Gromov11], and then was developed and studied systematically by Lindenstrauss and Weiss [Reference Lindenstrauss and Weiss26]. It is a numerical invariant, taking values in the range
![]() $[0, +\infty ]$
, to measure the complexity of
$[0, +\infty ]$
, to measure the complexity of
![]() $(X, \Gamma )$
in terms of dimension growth with respect to partial orbits. Applications of mean dimension theory can be found in the theory of topological dynamical systems (see [Reference Gutman12, Reference Gutman13, Reference Gutman and Tsukamoto15, Reference Gutman and Tsukamoto16, Reference Li22, Reference Lindenstrauss24, Reference Lindenstrauss and Weiss26]), geometric analysis (see [Reference Da Costa3, Reference Matsuo and Tsukamoto27, Reference Tsukamoto39, Reference Tsukamoto40]), operator algebras (see [Reference Elliott and Niu7, Reference Li and Liang23, Reference Niu28–Reference Phillips30]), and information theory (see [Reference Lindenstrauss and Tsukamoto25]).
$(X, \Gamma )$
in terms of dimension growth with respect to partial orbits. Applications of mean dimension theory can be found in the theory of topological dynamical systems (see [Reference Gutman12, Reference Gutman13, Reference Gutman and Tsukamoto15, Reference Gutman and Tsukamoto16, Reference Li22, Reference Lindenstrauss24, Reference Lindenstrauss and Weiss26]), geometric analysis (see [Reference Da Costa3, Reference Matsuo and Tsukamoto27, Reference Tsukamoto39, Reference Tsukamoto40]), operator algebras (see [Reference Elliott and Niu7, Reference Li and Liang23, Reference Niu28–Reference Phillips30]), and information theory (see [Reference Lindenstrauss and Tsukamoto25]).
On the other hand, for a general unital stably finite C*-algebra A, the radius of comparison, introduced by Toms [Reference Toms36] and denoted by
![]() $\mathrm {rc}(A)$
, is also a numerical invariant, to measure the regularity of the C*-algebra A. It can be regarded as an abstract measure of the dimension growth of A. A heuristic example is
$\mathrm {rc}(A)$
, is also a numerical invariant, to measure the regularity of the C*-algebra A. It can be regarded as an abstract measure of the dimension growth of A. A heuristic example is
![]() $\mathrm {M}_n(\mathrm {C}(X))$
, the C*-algebra of (complex)
$\mathrm {M}_n(\mathrm {C}(X))$
, the C*-algebra of (complex)
![]() $n \times n$
matrix valued continuous functions on a finite CW-complex X; its radius of comparison is around
$n \times n$
matrix valued continuous functions on a finite CW-complex X; its radius of comparison is around
![]() $\frac {1}{2} \frac {\mathrm {dim}(X)}{n}$
, half the dimension ratio of
$\frac {1}{2} \frac {\mathrm {dim}(X)}{n}$
, half the dimension ratio of
![]() $\mathrm {M}_n(\mathrm {C}(X))$
.
$\mathrm {M}_n(\mathrm {C}(X))$
.
For the given topological dynamical system
![]() $(X, \Gamma )$
, the canonical C*-algebra to be considered is the transformation group C*-algebra,
$(X, \Gamma )$
, the canonical C*-algebra to be considered is the transformation group C*-algebra,
![]() $\mathrm {C}(X) \rtimes \Gamma $
. A natural question to ask then is how the radius of comparison of the C*-algebra is connected to the mean dimension of the dynamical system. Phillips and Toms have made the following conjecture:
$\mathrm {C}(X) \rtimes \Gamma $
. A natural question to ask then is how the radius of comparison of the C*-algebra is connected to the mean dimension of the dynamical system. Phillips and Toms have made the following conjecture:
Conjecture (Phillips–Toms)
Let
![]() $(X, \Gamma )$
be a minimal and free topological dynamical system, where X is a compact Hausdorff space, and
$(X, \Gamma )$
be a minimal and free topological dynamical system, where X is a compact Hausdorff space, and
![]() $\Gamma $
is a discrete amenable group. Then
$\Gamma $
is a discrete amenable group. Then
This conjecture is closely related to the classification of C*-algebras. In general, the C*-algebra
![]() $\mathrm {C}(X)\rtimes \Gamma $
can be wild and not determined by (i.e., classified by) the Elliott invariant (even with
$\mathrm {C}(X)\rtimes \Gamma $
can be wild and not determined by (i.e., classified by) the Elliott invariant (even with
![]() $\Gamma =\mathbb Z$
; see [Reference Giol and Kerr8]). So, an important question in the classification program for C*-algebras is to determine which transformation group C*-algebras are classifiable. Now, a special case of this conjecture is that
$\Gamma =\mathbb Z$
; see [Reference Giol and Kerr8]). So, an important question in the classification program for C*-algebras is to determine which transformation group C*-algebras are classifiable. Now, a special case of this conjecture is that
![]() $\mathrm {mdim}(X, \Gamma ) = 0$
implies
$\mathrm {mdim}(X, \Gamma ) = 0$
implies
![]() $\mathrm {rc}(\mathrm {C}(X)\rtimes \Gamma ) = 0$
, which is the same as strict comparison of positive elements; by the Toms–Winter conjecture, this should imply that the C*-algebra
$\mathrm {rc}(\mathrm {C}(X)\rtimes \Gamma ) = 0$
, which is the same as strict comparison of positive elements; by the Toms–Winter conjecture, this should imply that the C*-algebra
![]() $\mathrm {C}(X)\rtimes \Gamma $
is Jiang–Su stable; and hence belongs to the classifiable class of [Reference Castillejos, Evington, Tikuisis, White and Winter2, Reference Elliott, Gong, Lin and Niu4, Reference Elliott, Niu, Doran and Park6, Reference Gong, Lin and Niu9, Reference Gong, Lin and Niu10, Reference Tikuisis, White and Winter35].
$\mathrm {C}(X)\rtimes \Gamma $
is Jiang–Su stable; and hence belongs to the classifiable class of [Reference Castillejos, Evington, Tikuisis, White and Winter2, Reference Elliott, Gong, Lin and Niu4, Reference Elliott, Niu, Doran and Park6, Reference Gong, Lin and Niu9, Reference Gong, Lin and Niu10, Reference Tikuisis, White and Winter35].
Many researches have been done on the classifiability of transformation group C*-algebras. Under the assumption that X is finite dimensional (in which case the mean dimension is automatically zero), it was shown in [Reference Toms and Winter38] that the algebra
![]() $\mathrm {C}(X)\rtimes \mathbb Z$
has finite nuclear dimension, and therefore is Jiang–Su stable. Using Rokhlin dimension, this result was generalized to
$\mathrm {C}(X)\rtimes \mathbb Z$
has finite nuclear dimension, and therefore is Jiang–Su stable. Using Rokhlin dimension, this result was generalized to
![]() $\mathrm {C}(X)\rtimes \mathbb Z^d$
by [Reference Szabó33], and then to the actions of residually finite groups with box spaces of finite asymptotic dimension (see [Reference Szabo, Wu and Zacharias34]). And recently, substantial progresses have been made on the Jiang–Su stability using almost finiteness and dynamical comparison (see [Reference Kerr18–Reference Kerr and Szabó20]).
$\mathrm {C}(X)\rtimes \mathbb Z^d$
by [Reference Szabó33], and then to the actions of residually finite groups with box spaces of finite asymptotic dimension (see [Reference Szabo, Wu and Zacharias34]). And recently, substantial progresses have been made on the Jiang–Su stability using almost finiteness and dynamical comparison (see [Reference Kerr18–Reference Kerr and Szabó20]).
In the case that X is not necessary finite dimensional, which this paper mainly focuses on, so far the only result is [Reference Elliott and Niu7] where
![]() $\mathbb Z$
-actions were considered, and zero mean dimension was shown to imply zero radius of comparison (classifiability of the C*-algebra). Note that this result in particular covers all strictly ergodic dynamical systems. Beyond the case of mean dimension zero, Phillips considered
$\mathbb Z$
-actions were considered, and zero mean dimension was shown to imply zero radius of comparison (classifiability of the C*-algebra). Note that this result in particular covers all strictly ergodic dynamical systems. Beyond the case of mean dimension zero, Phillips considered
![]() $\mathbb Z$
-actions in [Reference Phillips30] and showed that (in the minimal case) the radius of comparison of
$\mathbb Z$
-actions in [Reference Phillips30] and showed that (in the minimal case) the radius of comparison of
![]() $\mathrm {C}(X) \rtimes \mathbb Z$
is at most
$\mathrm {C}(X) \rtimes \mathbb Z$
is at most
![]() $1+36\mathrm {mdim}(X, \mathbb Z)$
.
$1+36\mathrm {mdim}(X, \mathbb Z)$
.
In this paper, the results of [Reference Elliott and Niu7] are both strengthened and generalized to minimal and free
![]() $\mathbb Z^d$
-actions.
$\mathbb Z^d$
-actions.
Theorem A (Theorem 5.6)
Let
![]() $(X, T, \mathbb Z^d)$
be a minimal-free dynamical system. Then
$(X, T, \mathbb Z^d)$
be a minimal-free dynamical system. Then
As a consequence, one obtains classifiability of
![]() $\mathrm {C}(X)\rtimes \mathbb Z^d$
if
$\mathrm {C}(X)\rtimes \mathbb Z^d$
if
![]() $(X, T, \mathbb Z^d)$
has mean dimension zero.
$(X, T, \mathbb Z^d)$
has mean dimension zero.
Theorem B (Theorem 5.8)
Let
![]() $(X, T, \mathbb Z^d)$
be a minimal-free dynamical system with mean dimension zero. Then
$(X, T, \mathbb Z^d)$
be a minimal-free dynamical system with mean dimension zero. Then
![]() $\mathrm {C}(X) \rtimes \mathbb Z^d$
absorbs the Jiang–Su algebra tensorially, and hence is classified by its Elliott invariant. In particular, if
$\mathrm {C}(X) \rtimes \mathbb Z^d$
absorbs the Jiang–Su algebra tensorially, and hence is classified by its Elliott invariant. In particular, if
![]() $\mathrm {dim}(X) < \infty $
, or
$\mathrm {dim}(X) < \infty $
, or
![]() $(X, T, \mathbb Z^d)$
has at most countably many ergodic measures, or
$(X, T, \mathbb Z^d)$
has at most countably many ergodic measures, or
![]() $(X, T, \mathbb Z^d)$
has finite topological entropy, then
$(X, T, \mathbb Z^d)$
has finite topological entropy, then
![]() $\mathrm {C}(X) \rtimes \mathbb Z^d$
is classified by its Elliott invariant.
$\mathrm {C}(X) \rtimes \mathbb Z^d$
is classified by its Elliott invariant.
The argument in [Reference Elliott and Niu7, Reference Phillips30, Reference Toms and Winter38] relies on Putnam’s orbit-cutting algebra (or what Phillips termed the large subalgebra)
![]() $A_y$
, associated with a point
$A_y$
, associated with a point
![]() $y\in X$
. In the case of zero mean dimension, the argument in [Reference Elliott and Niu7] also heavily depends on the small boundary property (which is equivalent to mean dimension zero in the case of
$y\in X$
. In the case of zero mean dimension, the argument in [Reference Elliott and Niu7] also heavily depends on the small boundary property (which is equivalent to mean dimension zero in the case of
![]() $\mathbb Z$
-actions). However, beyond the case of
$\mathbb Z$
-actions). However, beyond the case of
![]() $\mathbb Z$
-actions, it is not clear in general how to construct large subalgebras; moreover, once the dynamical system does not have mean dimension zero, the small boundary property does not hold any more. So, instead of large subalgebra and small boundary property, the proofs of Theorems A and B depend on the Uniform Rokhlin Property (URP) and Cuntz-comparison of open sets (COS).
$\mathbb Z$
-actions, it is not clear in general how to construct large subalgebras; moreover, once the dynamical system does not have mean dimension zero, the small boundary property does not hold any more. So, instead of large subalgebra and small boundary property, the proofs of Theorems A and B depend on the Uniform Rokhlin Property (URP) and Cuntz-comparison of open sets (COS).
Definition 1.1. (Definitions 3.1 and 4.1 of [Reference Niu29])
A topological dynamical system
![]() $(X, \Gamma )$
, where
$(X, \Gamma )$
, where
![]() $\Gamma $
is a discrete amenable group, is said to have the URP if, for any
$\Gamma $
is a discrete amenable group, is said to have the URP if, for any
![]() $\varepsilon>0$
and any finite set
$\varepsilon>0$
and any finite set
![]() $K\subseteq \Gamma $
, there exist closed sets
$K\subseteq \Gamma $
, there exist closed sets
![]() $B_1, B_2, \ldots , B_S \subseteq X$
and
$B_1, B_2, \ldots , B_S \subseteq X$
and
![]() $(K, \varepsilon )$
-invariant sets
$(K, \varepsilon )$
-invariant sets
![]() $\Gamma _1, \Gamma _2, \ldots , \Gamma _S \subseteq \Gamma $
such that the sets
$\Gamma _1, \Gamma _2, \ldots , \Gamma _S \subseteq \Gamma $
such that the sets
are mutually disjoint and
 $$ \begin{align*}\mathrm{ocap}(X\setminus\bigsqcup_{s=1}^S\bigsqcup_{\gamma\in \Gamma_s}B_s\gamma) < \varepsilon,\end{align*} $$
$$ \begin{align*}\mathrm{ocap}(X\setminus\bigsqcup_{s=1}^S\bigsqcup_{\gamma\in \Gamma_s}B_s\gamma) < \varepsilon,\end{align*} $$
where
![]() $\mathrm {ocap}$
denotes the orbit capacity (see, for instance, Definition 5.1 of [Reference Lindenstrauss and Weiss26]).
$\mathrm {ocap}$
denotes the orbit capacity (see, for instance, Definition 5.1 of [Reference Lindenstrauss and Weiss26]).
The dynamical system
![]() $(X, \Gamma )$
is said to have
$(X, \Gamma )$
is said to have
![]() $(\lambda , m)$
-COS, where
$(\lambda , m)$
-COS, where
![]() $\lambda \in (0, 1]$
and
$\lambda \in (0, 1]$
and
![]() $m\in \mathbb N$
, if for any open sets
$m\in \mathbb N$
, if for any open sets
![]() $E, F\subseteq X$
with
$E, F\subseteq X$
with
where
![]() $\mathcal {M}_1(X, \Gamma )$
is the simplex of all invariant probability measures on X, then
$\mathcal {M}_1(X, \Gamma )$
is the simplex of all invariant probability measures on X, then
 $$ \begin{align*}\varphi_E \precsim \underbrace{\varphi_F\oplus\cdots \oplus \varphi_F}_m\quad\mathrm{in}\ (\mathrm{C}(X)\rtimes\Gamma)\otimes\mathcal K,\end{align*} $$
$$ \begin{align*}\varphi_E \precsim \underbrace{\varphi_F\oplus\cdots \oplus \varphi_F}_m\quad\mathrm{in}\ (\mathrm{C}(X)\rtimes\Gamma)\otimes\mathcal K,\end{align*} $$
where
![]() $\varphi _E$
and
$\varphi _E$
and
![]() $\varphi _F$
are continuous functions supported on E and F, respectively (see Example 2.1).
$\varphi _F$
are continuous functions supported on E and F, respectively (see Example 2.1).
The dynamical system
![]() $(X, \Gamma )$
is said to have COS if it has
$(X, \Gamma )$
is said to have COS if it has
![]() $(\lambda , m)$
-COS for some
$(\lambda , m)$
-COS for some
![]() $\lambda $
and m.
$\lambda $
and m.
Remark 1.2. If
![]() $\Gamma $
is monotilable, e.g.,
$\Gamma $
is monotilable, e.g.,
![]() $\Gamma =\mathbb Z^d$
, then one can take
$\Gamma =\mathbb Z^d$
, then one can take
![]() $S=1$
in the definition of URP.
$S=1$
in the definition of URP.
These properties were introduced in [Reference Niu29], and it was shown (Theorem 4.8 of [Reference Niu29]) that the URP and COS together imply
if
![]() $(X, \Gamma )$
is free and minimal. It was shown in [Reference Niu28] (Theorem 4.8) that if, in addition,
$(X, \Gamma )$
is free and minimal. It was shown in [Reference Niu28] (Theorem 4.8) that if, in addition,
![]() $(X, \Gamma )$
has mean dimension zero, then the C*-algebra
$(X, \Gamma )$
has mean dimension zero, then the C*-algebra
![]() $\mathrm {C}(X)\rtimes \Gamma $
is classifiable. Thus, both Theorems A and B follow from the following result.
$\mathrm {C}(X)\rtimes \Gamma $
is classifiable. Thus, both Theorems A and B follow from the following result.
Theorem C (Theorems 4.2 and 5.5)
Any dynamical system
![]() $(X, T, \mathbb Z^d)$
with the marker property (see Definition 3.1) has the URP and COS.
$(X, T, \mathbb Z^d)$
with the marker property (see Definition 3.1) has the URP and COS.
The proof of the theorem above uses the adding-one-dimension and going-down arguments of [Reference Gutman, Lindenstrauss and Tsukamoto14]. With these arguments, one constructs a Rokhlin tower with base set open, such that the tower almost cover the whole space in the sense that the its complement is uniformly small under all the invariant probability measures. This implies the property URP, and is essentially contained in [Reference Gutman, Lindenstrauss and Tsukamoto14].
For the property COS, one actually uses the adding-one-dimension and going-down arguments to construct two Rokhlin towers. Although these two Rokhlin towers do not in general even taken together cover the space X (even approximately), they can be constructed so that the complement of the first tower can be broken into finitely many pieces so that each piece can be translated into the support of the second tower, in such a way that the (order of the) overlaps of the translations of those pieces can be bounded by a constant which only depends on the group
![]() $\mathbb Z^d$
. Together with other things, this eventually leads to the property COS.
$\mathbb Z^d$
. Together with other things, this eventually leads to the property COS.
Remark 1.3. In [Reference Li and Niu21], it is shown that the URP and COS imply that the C*-algebra
![]() $\mathrm {C}(X)\rtimes \Gamma $
always has stable rank one (classifiable or not), and satisfies the Toms–Winter conjecture (i.e., it is classifiable if, and only if it has strict comparison of positive elements) if
$\mathrm {C}(X)\rtimes \Gamma $
always has stable rank one (classifiable or not), and satisfies the Toms–Winter conjecture (i.e., it is classifiable if, and only if it has strict comparison of positive elements) if
![]() $(X, \Gamma )$
is free and minimal. Thus, by Theorem C, the C*-algebra
$(X, \Gamma )$
is free and minimal. Thus, by Theorem C, the C*-algebra
![]() $\mathrm {C}(X)\rtimes \mathbb Z^d$
always has stable rank one (classifiable or not), and satisfies the Toms–Winter conjecture. (In [Reference Alboiu and Lutley1], stable rank one was established in the case
$\mathrm {C}(X)\rtimes \mathbb Z^d$
always has stable rank one (classifiable or not), and satisfies the Toms–Winter conjecture. (In [Reference Alboiu and Lutley1], stable rank one was established in the case
![]() $d=1$
.)
$d=1$
.)
2 Notation and preliminaries
2.1 Topological dynamical systems
In this paper, we shall only consider
![]() $\mathbb Z^d$
-actions on a metrizable compact Hausdorff space X.
$\mathbb Z^d$
-actions on a metrizable compact Hausdorff space X.
Definition 2.1. Consider a topological dynamical system
![]() $(X, T, \mathbb Z^d)$
. A closed set
$(X, T, \mathbb Z^d)$
. A closed set
![]() $Y \subseteq X$
is said to be invariant if
$Y \subseteq X$
is said to be invariant if
![]() $T^n(Y) = Y$
,
$T^n(Y) = Y$
,
![]() $n \in \mathbb Z^d$
, and
$n \in \mathbb Z^d$
, and
![]() $(X, T, \mathbb Z^d)$
is said to be minimal if
$(X, T, \mathbb Z^d)$
is said to be minimal if
![]() $\varnothing $
and X are the only invariant closed subsets. The dynamical system
$\varnothing $
and X are the only invariant closed subsets. The dynamical system
![]() $(X, T, \mathbb Z^d)$
is free if for any
$(X, T, \mathbb Z^d)$
is free if for any
![]() $x\in X$
,
$x\in X$
,
![]() $\{n\in \mathbb Z^d: T^n(x) = x\} = \{0\}$
.
$\{n\in \mathbb Z^d: T^n(x) = x\} = \{0\}$
.
Remark 2.2. The dynamical system
![]() $(X, T, \mathbb Z^d)$
is induced by d commuting homeomorphisms of X, and vice versa.
$(X, T, \mathbb Z^d)$
is induced by d commuting homeomorphisms of X, and vice versa.
Definition 2.3. A Borel measure
![]() $\mu $
on X is invariant under the action
$\mu $
on X is invariant under the action
![]() $\sigma $
if
$\sigma $
if
![]() $\mu (E) = \mu (T^n(E))$
, for any
$\mu (E) = \mu (T^n(E))$
, for any
![]() $n\in \mathbb Z^d$
and any Borel set
$n\in \mathbb Z^d$
and any Borel set
![]() $E\subseteq X$
. Denote by
$E\subseteq X$
. Denote by
![]() $\mathcal M_1(X, T, \mathbb Z^d)$
, the collection of all invariant Borel probability measures on X. It is a Choquet simplex under the weak* topology.
$\mathcal M_1(X, T, \mathbb Z^d)$
, the collection of all invariant Borel probability measures on X. It is a Choquet simplex under the weak* topology.
Definition 2.4. (See [Reference Gromov11, Reference Lindenstrauss and Weiss26])
Consider a topological dynamical system
![]() $(X, T, \mathbb Z^d)$
, and let E be a subset of X. The orbit capacity of E is defined by
$(X, T, \mathbb Z^d)$
, and let E be a subset of X. The orbit capacity of E is defined by
 $$\begin{align*}\mathrm{ocap}(E):=\lim_{N\to\infty}\frac{1}{N^d}\sup_{x\in X}\sum_{n\in\{0, 1, \ldots, N-1\}^d} \chi_E(T^n(x)),\end{align*}$$
$$\begin{align*}\mathrm{ocap}(E):=\lim_{N\to\infty}\frac{1}{N^d}\sup_{x\in X}\sum_{n\in\{0, 1, \ldots, N-1\}^d} \chi_E(T^n(x)),\end{align*}$$
where
![]() $\chi _E$
is the characteristic function of E. The limit always exists.
$\chi _E$
is the characteristic function of E. The limit always exists.
Definition 2.5. (See [Reference Lindenstrauss and Weiss26])
Let
![]() $\mathcal U$
be an open cover of X. Define
$\mathcal U$
be an open cover of X. Define
where
![]() $\mathrm {ord}(\mathcal V):=-1 + \sup _{x\in X}\sum _{V\in \mathcal V} \chi _V(x)$
.
$\mathrm {ord}(\mathcal V):=-1 + \sup _{x\in X}\sum _{V\in \mathcal V} \chi _V(x)$
.
Consider a topological dynamical system
![]() $(X, T, \mathbb Z^d)$
. Then the topological mean dimension of
$(X, T, \mathbb Z^d)$
. Then the topological mean dimension of
![]() $(X, T, \mathbb Z^d)$
is defined by
$(X, T, \mathbb Z^d)$
is defined by
 $$ \begin{align*}\mathrm{mdim}(X, T, \mathbb Z^d):=\sup_{\mathcal U}\lim_{N\to\infty}\frac{1}{N^d}D(\bigvee_{n\in\{0, 1, \ldots, N-1\}^d} T^{-n}(\mathcal U)),\end{align*} $$
$$ \begin{align*}\mathrm{mdim}(X, T, \mathbb Z^d):=\sup_{\mathcal U}\lim_{N\to\infty}\frac{1}{N^d}D(\bigvee_{n\in\{0, 1, \ldots, N-1\}^d} T^{-n}(\mathcal U)),\end{align*} $$
where
![]() $\mathcal U$
runs over all finite open covers of X.
$\mathcal U$
runs over all finite open covers of X.
Remark 2.6. It follows from the definition that if
![]() $\mathrm {dim}(X) < \infty $
, then
$\mathrm {dim}(X) < \infty $
, then
![]() $\mathrm {mdim}(X, T, \mathbb Z^d)=0$
. By [Reference Lindenstrauss and Weiss26], if
$\mathrm {mdim}(X, T, \mathbb Z^d)=0$
. By [Reference Lindenstrauss and Weiss26], if
![]() $(X, T, \mathbb Z^d)$
has at most countably many ergodic measures, then
$(X, T, \mathbb Z^d)$
has at most countably many ergodic measures, then
![]() $\mathrm {mdim}(X, T, \mathbb Z^d)=0$
. Also by [Reference Lindenstrauss24], if
$\mathrm {mdim}(X, T, \mathbb Z^d)=0$
. Also by [Reference Lindenstrauss24], if
![]() $(X, T, \mathbb Z^d)$
has finite topological entropy, then
$(X, T, \mathbb Z^d)$
has finite topological entropy, then
![]() $\mathrm {mdim}(X, T, \mathbb Z^d)=0$
.
$\mathrm {mdim}(X, T, \mathbb Z^d)=0$
.
Definition 2.7. (Definition 3.1 of [Reference Niu29] and Remark 1.2)
A topological dynamical system
![]() $(X, T, \mathbb Z^d)$
is said to have the URP if for any
$(X, T, \mathbb Z^d)$
is said to have the URP if for any
![]() $\varepsilon>0$
and any
$\varepsilon>0$
and any
![]() $N\in \mathbb {N}$
, there exists a closed set
$N\in \mathbb {N}$
, there exists a closed set
![]() $B \subseteq X$
such that the sets
$B \subseteq X$
such that the sets
are mutually disjoint and
In this paper, we shall show that all minimal and free dynamical systems
![]() $(X, T, \mathbb Z^d)$
have the property URP (Theorem 4.2).
$(X, T, \mathbb Z^d)$
have the property URP (Theorem 4.2).
2.2 Crossed product C*-algebras
Let
![]() $(X, T, \mathbb Z^d)$
be a topological dynamical system. Then the crossed product C*-algebra
$(X, T, \mathbb Z^d)$
be a topological dynamical system. Then the crossed product C*-algebra
![]() $\mathrm {C}(X)\rtimes \mathbb Z^d$
is the universal C*-algebra
$\mathrm {C}(X)\rtimes \mathbb Z^d$
is the universal C*-algebra
The C*-algebra A is nuclear, and if T is minimal and free, the C*-algebra A is simple. Moreover, the simplex of tracial states of
![]() $\mathrm {C}(X) \rtimes _\sigma \Gamma $
is canonically homeomorphic to the simplex of invariant probability measures of
$\mathrm {C}(X) \rtimes _\sigma \Gamma $
is canonically homeomorphic to the simplex of invariant probability measures of
![]() $(X, T, \mathbb Z^d)$
.
$(X, T, \mathbb Z^d)$
.
2.3 Cuntz comparison of positive elements of a C*-algebra
Definition 2.8. Let A be a C*-algebra, and let
![]() $a, b\in A^+$
. Then we say that a is Cuntz subequivalent to b, denoted by
$a, b\in A^+$
. Then we say that a is Cuntz subequivalent to b, denoted by
![]() $a \precsim b$
, if there are
$a \precsim b$
, if there are
![]() $x_i$
,
$x_i$
,
![]() $y_i$
,
$y_i$
,
![]() $i=1, 2, \ldots $
, such that
$i=1, 2, \ldots $
, such that
We say that a is Cuntz equivalent to b if
![]() $a\precsim b$
and
$a\precsim b$
and
![]() $b \precsim a$
. This is an equivalence relation; let us denote the equivalence class of a by
$b \precsim a$
. This is an equivalence relation; let us denote the equivalence class of a by
![]() $[a]$
.
$[a]$
.
Let
![]() $\mathcal K$
denote the algebra of compact operators on a separable Hilbert space. Then the equivalence classes of positive elements of
$\mathcal K$
denote the algebra of compact operators on a separable Hilbert space. Then the equivalence classes of positive elements of
![]() $A\otimes \mathcal K$
form an ordered semigroup under the addition
$A\otimes \mathcal K$
form an ordered semigroup under the addition
 $$ \begin{align*}[a] + [b] := \left[\left(\begin{array}{cc} a & \\ & b \end{array}\right)\right],\quad a, b \in (A\otimes\mathcal K)^+\end{align*} $$
$$ \begin{align*}[a] + [b] := \left[\left(\begin{array}{cc} a & \\ & b \end{array}\right)\right],\quad a, b \in (A\otimes\mathcal K)^+\end{align*} $$
(independent of the isomorphism
![]() $\mathcal K \cong \mathcal K \otimes \mathrm {M}_2$
). It is called the Cuntz semigroup of A.
$\mathcal K \cong \mathcal K \otimes \mathrm {M}_2$
). It is called the Cuntz semigroup of A.
Let
![]() $\tau : A \to \mathbb C$
be a trace. Define the rank function
$\tau : A \to \mathbb C$
be a trace. Define the rank function
where
![]() $\mu _\tau $
is the Borel measure induced by
$\mu _\tau $
is the Borel measure induced by
![]() $\tau $
on the spectrum of a. It is well known that
$\tau $
on the spectrum of a. It is well known that
Example 2.1. Consider
![]() $h\in \mathrm {C}(X)^+$
and let
$h\in \mathrm {C}(X)^+$
and let
![]() $\mu $
be a probability measure on X. Then
$\mu $
be a probability measure on X. Then
where
![]() $\tau _\mu $
is the trace of
$\tau _\mu $
is the trace of
![]() $\mathrm {C}(X)$
induced by
$\mathrm {C}(X)$
induced by
![]() $\mu $
.
$\mu $
.
Let
![]() $f, g\in \mathrm {C}(X)$
be positive elements. Then f and g are Cuntz equivalent if and only if
$f, g\in \mathrm {C}(X)$
be positive elements. Then f and g are Cuntz equivalent if and only if
![]() $f^{-1}(0, +\infty )= g^{-1}(0, +\infty )$
. That is, their equivalence classes are determined by their open supports.
$f^{-1}(0, +\infty )= g^{-1}(0, +\infty )$
. That is, their equivalence classes are determined by their open supports.
With this example, let us introduce the following notation.
Definition 2.9. For each open set
![]() $E \subseteq X$
, pick a continuous function
$E \subseteq X$
, pick a continuous function
For instance, one can pick
![]() $\varphi _E(x) = d(x, X\setminus E)$
, where d is a compatible metric on X. This notation will be used throughout this paper. Note that the Cuntz equivalence class of
$\varphi _E(x) = d(x, X\setminus E)$
, where d is a compatible metric on X. This notation will be used throughout this paper. Note that the Cuntz equivalence class of
![]() $\varphi _E$
is independent of the choice of the individual function
$\varphi _E$
is independent of the choice of the individual function
![]() $\varphi _E$
.
$\varphi _E$
.
In general, the converse of (2.1) fails (e.g.,
![]() $A = \mathrm {M}_4(\mathrm {C}(S^2\times S^2))$
). But one can measure it by the radius of comparison.
$A = \mathrm {M}_4(\mathrm {C}(S^2\times S^2))$
). But one can measure it by the radius of comparison.
Definition 2.10. (Definition 6.1 of [Reference Toms36])
Let A be a C*-algebra. Denote by
![]() $\mathrm {M}_n(A)$
, the C*-algebra of
$\mathrm {M}_n(A)$
, the C*-algebra of
![]() $n\times n$
matrices over A. Regard
$n\times n$
matrices over A. Regard
![]() $\mathrm {M}_n(A)$
as the upper-left corner of
$\mathrm {M}_n(A)$
as the upper-left corner of
![]() $\mathrm {M}_{n+1}(A)$
, and consider the union
$\mathrm {M}_{n+1}(A)$
, and consider the union
the algebra of all finite matrices over A.
The radius of comparison of a unital C*-algebra A, denoted by
![]() $\mathrm {rc}(A)$
, is the infimum of the set of real numbers
$\mathrm {rc}(A)$
, is the infimum of the set of real numbers
![]() $r> 0$
such that if
$r> 0$
such that if
![]() $a, b\in (\mathrm {M}_\infty (A))^+$
satisfy
$a, b\in (\mathrm {M}_\infty (A))^+$
satisfy
then
![]() $a \precsim b$
, where
$a \precsim b$
, where
![]() $\mathrm {T}(A)$
is the simplex of tracial states. (In [Reference Toms36], the radius of comparison is defined in terms of quasitraces instead of traces; but since all the algebras considered in this note are nuclear, by [Reference Haagerup17], any quasitrace actually is a trace.)
$\mathrm {T}(A)$
is the simplex of tracial states. (In [Reference Toms36], the radius of comparison is defined in terms of quasitraces instead of traces; but since all the algebras considered in this note are nuclear, by [Reference Haagerup17], any quasitrace actually is a trace.)
Example 2.2. Let X be a compact Hausdorff space. Then (see [Reference Toms37])
where
![]() $\mathrm {dim(X)}$
is the topological covering dimension of X (a lower bound for
$\mathrm {dim(X)}$
is the topological covering dimension of X (a lower bound for
![]() $\mathrm {rc}(\mathrm {C}(X))$
in terms of cohomological dimension is given in [Reference Elliott and Niu5]).
$\mathrm {rc}(\mathrm {C}(X))$
in terms of cohomological dimension is given in [Reference Elliott and Niu5]).
The C*-algebra
![]() $\mathrm {C}(X)$
is canonically contained in the crossed product C*-algebra
$\mathrm {C}(X)$
is canonically contained in the crossed product C*-algebra
![]() $\mathrm {C}(X)\rtimes \mathbb Z^d$
. Thus, one can compare positive elements of
$\mathrm {C}(X)\rtimes \mathbb Z^d$
. Thus, one can compare positive elements of
![]() $\mathrm {C}(X)$
not only inside
$\mathrm {C}(X)$
not only inside
![]() $\mathrm {C}(X)$
, but also inside the larger C*-algebra
$\mathrm {C}(X)$
, but also inside the larger C*-algebra
![]() $\mathrm {C}(X)\rtimes \mathbb Z^d$
.
$\mathrm {C}(X)\rtimes \mathbb Z^d$
.
Definition 2.11. (Definition 4.1 of [Reference Niu29])
A dynamical system
![]() $(X, T, \mathbb Z^d)$
is said to have
$(X, T, \mathbb Z^d)$
is said to have
![]() $(\lambda , m)$
-COS, where
$(\lambda , m)$
-COS, where
![]() $\lambda \in (0, 1]$
and
$\lambda \in (0, 1]$
and
![]() $m\in \mathbb N$
, if for any open sets
$m\in \mathbb N$
, if for any open sets
![]() $E, F\subseteq X$
with
$E, F\subseteq X$
with
then
 $$ \begin{align*}\varphi_E \precsim \underbrace{\varphi_F\oplus\cdots \oplus \varphi_F}_m\quad\mathrm{in}\ (\mathrm{C}(X)\rtimes\mathbb Z^d)\otimes\mathcal K,\end{align*} $$
$$ \begin{align*}\varphi_E \precsim \underbrace{\varphi_F\oplus\cdots \oplus \varphi_F}_m\quad\mathrm{in}\ (\mathrm{C}(X)\rtimes\mathbb Z^d)\otimes\mathcal K,\end{align*} $$
where
![]() $\varphi _E $
and
$\varphi _E $
and
![]() $\varphi _F$
are continuous functions given by Definition 2.9.
$\varphi _F$
are continuous functions given by Definition 2.9.
The dynamical system
![]() $(X, \Gamma )$
is said to have COS if it has
$(X, \Gamma )$
is said to have COS if it has
![]() $(\lambda , m)$
-COS for some
$(\lambda , m)$
-COS for some
![]() $\lambda $
and m.
$\lambda $
and m.
In this paper, we shall show that all minimal and free dynamical systems
![]() $(X, T, \mathbb Z^d)$
have the property COS (Theorem 5.5). Together with the property URP, we obtain a dynamical version of (2.2); that is,
$(X, T, \mathbb Z^d)$
have the property COS (Theorem 5.5). Together with the property URP, we obtain a dynamical version of (2.2); that is,
if
![]() $(X, T, \mathbb Z^d)$
is minimal and free (Corollary 5.6).
$(X, T, \mathbb Z^d)$
is minimal and free (Corollary 5.6).
The following notation and lemma will be frequently used.
Definition 2.12. Let
![]() $a\in A^+$
, where A is a C*-algebra, and let
$a\in A^+$
, where A is a C*-algebra, and let
![]() $\varepsilon>0$
. Define
$\varepsilon>0$
. Define
where
![]() $f(t)=\max \{t-\varepsilon , 0\}$
.
$f(t)=\max \{t-\varepsilon , 0\}$
.
Lemma 2.13. (Section 2 of [Reference Rørdam31])
Let
![]() $a, b$
be positive elements of a C*-algebra A. Then
$a, b$
be positive elements of a C*-algebra A. Then
![]() $a \precsim b$
if and only if
$a \precsim b$
if and only if
![]() $(a-\varepsilon )_+ \precsim b$
for all
$(a-\varepsilon )_+ \precsim b$
for all
![]() $\varepsilon>0$
.
$\varepsilon>0$
.
3 Adding-one-dimension, going-down arguments, R-boundary points, and R-interior points
The adding-one-dimension and going-down arguments are introduced in [Reference Gutman, Lindenstrauss and Tsukamoto14], and they play a crucial role in the paper. Let us first make a brief review.
Definition 3.1. (Definition 1.2 of [Reference Gutman, Lindenstrauss and Tsukamoto14])
A topological dynamical system
![]() $(X, T, \Gamma )$
is said to have the marker property if, for any finite set
$(X, T, \Gamma )$
is said to have the marker property if, for any finite set
![]() $F\subseteq \Gamma $
, there is an open set
$F\subseteq \Gamma $
, there is an open set
![]() $U \subseteq X$
such that
$U \subseteq X$
such that
![]() $X = \bigcup _{n\in \Gamma } T^n(U)$
and
$X = \bigcup _{n\in \Gamma } T^n(U)$
and
![]() $U \cap T^n(U) = \varnothing $
for all nonidentity
$U \cap T^n(U) = \varnothing $
for all nonidentity
![]() $n\in F$
.
$n\in F$
.
Any topological dynamical system with the marker property is free; any minimal and free dynamical system has the marker property.
Let
![]() $(X, T, \mathbb Z^d)$
be a dynamical system with the marker property. Let M be an arbitrary natural number. Then there exist open set
$(X, T, \mathbb Z^d)$
be a dynamical system with the marker property. Let M be an arbitrary natural number. Then there exist open set
![]() $U\subseteq X$
, a compact set
$U\subseteq X$
, a compact set
![]() $K\subseteq U$
, an integer
$K\subseteq U$
, an integer
![]() $L>M$
, and a continuous function
$L>M$
, and a continuous function
![]() $\varphi : X \to [0, 1] $
with
$\varphi : X \to [0, 1] $
with
such that:
-
(1) if
 $\varphi (x)>0$
for some
$\varphi (x)>0$
for some
 $x\in X$
, then
$x\in X$
, then
 $\varphi (T^n(x))=0$
for all nonzero
$\varphi (T^n(x))=0$
for all nonzero
 $n\in \mathbb Z^d$
with
$n\in \mathbb Z^d$
with
 $\left \vert n\right \vert \leq M$
, and
$\left \vert n\right \vert \leq M$
, and -
(2) for any
 $x\in X$
, there is
$x\in X$
, there is
 $n\in \mathbb Z^d$
with
$n\in \mathbb Z^d$
with
 $\left \vert n\right \vert \leq L$
such that
$\left \vert n\right \vert \leq L$
such that
 $\varphi (T^n(x))=1$
.
$\varphi (T^n(x))=1$
.
See Section 4 of [Reference Gutman, Lindenstrauss and Tsukamoto14] for the proof.
Let
![]() $x\in X$
be arbitrary. Following [Reference Gutman, Lindenstrauss and Tsukamoto14], one considers the set
$x\in X$
be arbitrary. Following [Reference Gutman, Lindenstrauss and Tsukamoto14], one considers the set
and defines the Voronoi cell
![]() $V(x, n) \subseteq \mathbb R^{d+1}$
with center
$V(x, n) \subseteq \mathbb R^{d+1}$
with center
![]() $(n, \varphi (T^n(x))^{-1})$
by
$(n, \varphi (T^n(x))^{-1})$
by
where
![]() $\left \Vert \cdot \right \Vert $
is the
$\left \Vert \cdot \right \Vert $
is the
![]() $\ell ^2$
-norm on
$\ell ^2$
-norm on
![]() $\mathbb R^{d+1}$
. If
$\mathbb R^{d+1}$
. If
![]() $\varphi (T^n(x))=0$
, then put
$\varphi (T^n(x))=0$
, then put
One then has a tiling
Pick
![]() $H> (L+ \sqrt {d})^2$
. For each
$H> (L+ \sqrt {d})^2$
. For each
![]() $n\in \mathbb Z^{d}$
, define
$n\in \mathbb Z^{d}$
, define
One then has a tiling
The following are some basic properties of this construction, and the proofs can be found in [Reference Gutman, Lindenstrauss and Tsukamoto14].
Lemma 3.2. (Lemma 4.1 of [Reference Gutman, Lindenstrauss and Tsukamoto14])
With the construction above, one has:
-
(1)
 $\mathcal W_H$
is continuous on x in the following sense: Suppose that
$\mathcal W_H$
is continuous on x in the following sense: Suppose that
 $W(x, n)$
has nonempty interior. For any
$W(x, n)$
has nonempty interior. For any
 $\varepsilon>0$
, if
$\varepsilon>0$
, if
 $y\in X$
is sufficiently close to x, then the Hausdorff distance between
$y\in X$
is sufficiently close to x, then the Hausdorff distance between
 $W_H(x, n)$
and
$W_H(x, n)$
and
 $W_H(y, n)$
is less than
$W_H(y, n)$
is less than
 $\varepsilon $
.
$\varepsilon $
. -
(2)
 $\mathcal W_H$
is
$\mathcal W_H$
is
 $\mathbb Z^d$
-equivariant:
$\mathbb Z^d$
-equivariant:
 $W_H(T^m(x), n-m) = - m + W_H(x, n)$
.
$W_H(T^m(x), n-m) = - m + W_H(x, n)$
. -
(3) If
 $\varphi (T^n(x))> 0$
, then
$\varphi (T^n(x))> 0$
, then  $$ \begin{align*}B_{\frac{M}{2}}(n, \varphi(T^n(x))^{-1}) \subseteq V(x, n).\end{align*} $$
$$ \begin{align*}B_{\frac{M}{2}}(n, \varphi(T^n(x))^{-1}) \subseteq V(x, n).\end{align*} $$
-
(4) If
 $W_H(x, n)$
is nonempty, then
$W_H(x, n)$
is nonempty, then  $$ \begin{align*}1\leq \varphi(T^n(x))^{-1} \leq 2.\end{align*} $$
$$ \begin{align*}1\leq \varphi(T^n(x))^{-1} \leq 2.\end{align*} $$
-
(5) If
 $(a, -H) \in V(x, n)$
, then
$(a, -H) \in V(x, n)$
, then  $$ \begin{align*}\left\Vert a - n\right\Vert < L+\sqrt{d}.\end{align*} $$
$$ \begin{align*}\left\Vert a - n\right\Vert < L+\sqrt{d}.\end{align*} $$
Moreover, if one considers different horizontal cuts, at levels
![]() $-sH$
and
$-sH$
and
![]() $-H$
for some
$-H$
for some
![]() $s>1$
, then one has the following lemma.
$s>1$
, then one has the following lemma.
Lemma 3.3. (Lemma 4.1(4) of [Reference Gutman, Lindenstrauss and Tsukamoto14] and its proof)
Let
![]() $s>1$
and
$s>1$
and
![]() $r>0$
. One can choose M sufficiently large such that if
$r>0$
. One can choose M sufficiently large such that if
![]() $(a, -sH) \in V(x, n)$
, then
$(a, -sH) \in V(x, n)$
, then
and
 $$ \begin{align*}\left\Vert\frac{a}{s} + \left(1 - \frac{1}{s}\right)n - \left(a + \frac{(s-1)H}{sH+t}(n-a)\right)\right\Vert \leq \frac{4}{L+\sqrt{d}},\end{align*} $$
$$ \begin{align*}\left\Vert\frac{a}{s} + \left(1 - \frac{1}{s}\right)n - \left(a + \frac{(s-1)H}{sH+t}(n-a)\right)\right\Vert \leq \frac{4}{L+\sqrt{d}},\end{align*} $$
where
![]() $t= \varphi (T^n(x))^{-1}$
and
$t= \varphi (T^n(x))^{-1}$
and
![]() $\left \Vert \cdot \right \Vert $
is the
$\left \Vert \cdot \right \Vert $
is the
![]() $l^2$
-norm on
$l^2$
-norm on
![]() $\mathbb R^d$
.
$\mathbb R^d$
.
Definition 3.4. Note that the point
![]() $\left(a + \frac {(s-1)H}{sH+t}(n-a), -H\right)$
is the image of
$\left(a + \frac {(s-1)H}{sH+t}(n-a), -H\right)$
is the image of
![]() $(a, -sH)$
in the plane
$(a, -sH)$
in the plane
![]() $\mathbb R^d \times \{-H\}$
under the projection toward the center
$\mathbb R^d \times \{-H\}$
under the projection toward the center
![]() $(n, t)$
. Let us call
$(n, t)$
. Let us call
![]() $a + \frac {(s-1)H}{sH+t}(n-a)$
the H-projective image of a (with the center
$a + \frac {(s-1)H}{sH+t}(n-a)$
the H-projective image of a (with the center
![]() $(n, t)$
).
$(n, t)$
).
This construction can be illustrated by the following picture.

The following result concerns convex bodies in
![]() $\mathbb R^d$
; the author is indebted to Tyrrell McAllister for discussions related to this.
$\mathbb R^d$
; the author is indebted to Tyrrell McAllister for discussions related to this.
Lemma 3.5. Consider the Euclidean space
![]() $\mathbb R^d$
. For any
$\mathbb R^d$
. For any
![]() $\varepsilon>0$
and any
$\varepsilon>0$
and any
![]() $r>0$
, there is
$r>0$
, there is
![]() $N_0>0$
such that if
$N_0>0$
such that if
![]() $N\geq N_0$
, then, for any convex body
$N\geq N_0$
, then, for any convex body
![]() $V \subseteq \mathbb R^d$
, one has
$V \subseteq \mathbb R^d$
, one has
where
![]() $I_N = [0, N]^d$
.
$I_N = [0, N]^d$
.
Proof Pick
![]() $N_0$
sufficiently large that
$N_0$
sufficiently large that
 $$ \begin{align*}2 \frac{\mathrm{vol}(\partial_{r+\sqrt{d}}(I^r_N))}{\mathrm{vol}(I_N)} < \varepsilon,\quad N>N_0,\end{align*} $$
$$ \begin{align*}2 \frac{\mathrm{vol}(\partial_{r+\sqrt{d}}(I^r_N))}{\mathrm{vol}(I_N)} < \varepsilon,\quad N>N_0,\end{align*} $$
where
![]() $\partial _E(K)$
denotes the E-neighborhood of the boundary of a convex body K and
$\partial _E(K)$
denotes the E-neighborhood of the boundary of a convex body K and
![]() $I_N^r$
denotes the r-neighborhood of
$I_N^r$
denotes the r-neighborhood of
![]() $I_N$
. Then
$I_N$
. Then
![]() $N_0$
verifies the conclusion of the lemma.
$N_0$
verifies the conclusion of the lemma.
Indeed, for any
![]() $N\geq N_0$
, denote by
$N\geq N_0$
, denote by
![]() $\partial ^+_{r+\sqrt {d}}(V \cap I^r_N)$
, the outer
$\partial ^+_{r+\sqrt {d}}(V \cap I^r_N)$
, the outer
![]() $(r+\sqrt {d})$
-neighborhood of the convex body
$(r+\sqrt {d})$
-neighborhood of the convex body
![]() $V \cap I^r_N$
(i.e.,
$V \cap I^r_N$
(i.e.,
![]() $\partial ^+_{r+\sqrt {d}}(V \cap I^r_N) = (V \cap I^r_N)_{r+\sqrt {d}}\setminus V \cap I^r_N$
, where
$\partial ^+_{r+\sqrt {d}}(V \cap I^r_N) = (V \cap I^r_N)_{r+\sqrt {d}}\setminus V \cap I^r_N$
, where
![]() $(V \cap I^r_N)_{r+\sqrt {d}}$
denotes the
$(V \cap I^r_N)_{r+\sqrt {d}}$
denotes the
![]() $(r+\sqrt {d})$
-neighborhood of
$(r+\sqrt {d})$
-neighborhood of
![]() $V \cap I^r_N$
). It follows from Steiner’s formula (see, for instance, (4.1) of [Reference Schneider32]) and the fact that
$V \cap I^r_N$
). It follows from Steiner’s formula (see, for instance, (4.1) of [Reference Schneider32]) and the fact that
![]() $W_0(V \cap I^r_N) = \mathrm {vol}(V \cap I^r_N)$
that
$W_0(V \cap I^r_N) = \mathrm {vol}(V \cap I^r_N)$
that
 $$ \begin{align*}\mathrm{vol}(\partial^+_{r+\sqrt{d}}(V \cap I^r_N)) = \sum_{j=1}^d C_d^j W_j(V\cap I^r_N)(r+\sqrt{d})^j,\end{align*} $$
$$ \begin{align*}\mathrm{vol}(\partial^+_{r+\sqrt{d}}(V \cap I^r_N)) = \sum_{j=1}^d C_d^j W_j(V\cap I^r_N)(r+\sqrt{d})^j,\end{align*} $$
where
![]() $C_d^j = \frac {d!}{j!(d-j)!}$
and
$C_d^j = \frac {d!}{j!(d-j)!}$
and
![]() $W_j(\cdot )$
is the jth quermassintegral which can be written as
$W_j(\cdot )$
is the jth quermassintegral which can be written as
 $$ \begin{align*}W_j(K) = V(\underbrace{K, \ldots, K}_{d-j}, \underbrace{B, \ldots, B}_j)\end{align*} $$
$$ \begin{align*}W_j(K) = V(\underbrace{K, \ldots, K}_{d-j}, \underbrace{B, \ldots, B}_j)\end{align*} $$
for a convex body K with
![]() $V(\cdot )$
the mixed volume and B the unit ball of
$V(\cdot )$
the mixed volume and B the unit ball of
![]() $\mathbb R^d$
(see (5.31) of [Reference Schneider32]). Since the mixed volume is monotonic (see (5.25) of [Reference Schneider32]), the quermassintegrals
$\mathbb R^d$
(see (5.31) of [Reference Schneider32]). Since the mixed volume is monotonic (see (5.25) of [Reference Schneider32]), the quermassintegrals
![]() $W_j$
,
$W_j$
,
![]() $j=1, \ldots , d$
, are monotonic. Hence,
$j=1, \ldots , d$
, are monotonic. Hence,
and
 $$ \begin{align*} \mathrm{vol}(\partial^+_{r+\sqrt{d}}(V \cap I^r_N)) & = \sum_{j=1}^d C_d^j W_j(V\cap I^r_N)(r+\sqrt{d})^j \\ & \leq \sum_{j=1}^d C_d^j W_j(I^r_N)(r+\sqrt{d})^j \\ & = \mathrm{vol}(\partial^+_{r + \sqrt{d}}(I^r_N)). \end{align*} $$
$$ \begin{align*} \mathrm{vol}(\partial^+_{r+\sqrt{d}}(V \cap I^r_N)) & = \sum_{j=1}^d C_d^j W_j(V\cap I^r_N)(r+\sqrt{d})^j \\ & \leq \sum_{j=1}^d C_d^j W_j(I^r_N)(r+\sqrt{d})^j \\ & = \mathrm{vol}(\partial^+_{r + \sqrt{d}}(I^r_N)). \end{align*} $$
Since
![]() $\mathrm {vol}(\partial _{r+\sqrt {d}}(V\cap I^r_N)) \leq 2\mathrm {vol}(\partial ^+_{r+\sqrt {d}}(V\cap I^r_N))$
, one has
$\mathrm {vol}(\partial _{r+\sqrt {d}}(V\cap I^r_N)) \leq 2\mathrm {vol}(\partial ^+_{r+\sqrt {d}}(V\cap I^r_N))$
, one has
 $$ \begin{align*}\frac{\mathrm{vol}(\partial_{r+\sqrt{d}}(V\cap I^r_N))}{\mathrm{vol}(I_N)} \leq 2\frac{\mathrm{vol}(\partial^+_{r+\sqrt{d}}(V\cap I^r_N))}{\mathrm{vol}(I_N)} \leq 2 \frac{\mathrm{vol}(\partial_{r+\sqrt{d}}(I^r_N))}{\mathrm{vol}(I_N)} < \varepsilon.\end{align*} $$
$$ \begin{align*}\frac{\mathrm{vol}(\partial_{r+\sqrt{d}}(V\cap I^r_N))}{\mathrm{vol}(I_N)} \leq 2\frac{\mathrm{vol}(\partial^+_{r+\sqrt{d}}(V\cap I^r_N))}{\mathrm{vol}(I_N)} \leq 2 \frac{\mathrm{vol}(\partial_{r+\sqrt{d}}(I^r_N))}{\mathrm{vol}(I_N)} < \varepsilon.\end{align*} $$
On the other hand, note that,
and
![]() $(\partial _rV) \cap I_N$
is contained in the closed r-neighborhood of
$(\partial _rV) \cap I_N$
is contained in the closed r-neighborhood of
![]() $(\partial V) \cap I_N^{r}$
, one has that
$(\partial V) \cap I_N^{r}$
, one has that
![]() $(\partial _rV) \cap I_N$
is contained in the the closed r-neighborhood of
$(\partial _rV) \cap I_N$
is contained in the the closed r-neighborhood of
![]() $\partial (V \cap I_N^r)$
; that is,
$\partial (V \cap I_N^r)$
; that is,
Hence,
 $$ \begin{align*} & \left\vert\{n\in \mathbb Z^d: \mathrm{dist}(n, \partial V) \leq r,\ n\in I_N \}\right\vert \\ & \leq \left\vert \partial_r (V \cap I_N^r) \cap \mathbb Z^d\right\vert \\ & \leq \mathrm{vol}(\partial_{r+\sqrt{d}}(V\cap I^r_N)), \end{align*} $$
$$ \begin{align*} & \left\vert\{n\in \mathbb Z^d: \mathrm{dist}(n, \partial V) \leq r,\ n\in I_N \}\right\vert \\ & \leq \left\vert \partial_r (V \cap I_N^r) \cap \mathbb Z^d\right\vert \\ & \leq \mathrm{vol}(\partial_{r+\sqrt{d}}(V\cap I^r_N)), \end{align*} $$
so that
 $$ \begin{align*}\frac{1}{N^d}\left\vert\{n\in \mathbb Z^d: \mathrm{dist}(n, \partial V) \leq r,\ n\in I_N \}\right\vert \leq \frac{\mathrm{vol}(\partial_{r+\sqrt{d}}(V\cap I^r_N))}{\mathrm{vol}(I_N)} < \varepsilon,\end{align*} $$
$$ \begin{align*}\frac{1}{N^d}\left\vert\{n\in \mathbb Z^d: \mathrm{dist}(n, \partial V) \leq r,\ n\in I_N \}\right\vert \leq \frac{\mathrm{vol}(\partial_{r+\sqrt{d}}(V\cap I^r_N))}{\mathrm{vol}(I_N)} < \varepsilon,\end{align*} $$
as desired.
Definition 3.6. Consider a continuous function
![]() $X \ni x \mapsto \mathcal W(x)$
with
$X \ni x \mapsto \mathcal W(x)$
with
![]() $\mathcal W(x)$
an
$\mathcal W(x)$
an
![]() $\mathbb R^d$
-tiling. For each
$\mathbb R^d$
-tiling. For each
![]() $R \geq 0$
, a point
$R \geq 0$
, a point
![]() $x\in X$
is said to be an R-interior point if
$x\in X$
is said to be an R-interior point if
![]() $\mathrm {dist}(0, \partial \mathcal W(x))> R$
, where
$\mathrm {dist}(0, \partial \mathcal W(x))> R$
, where
![]() $\partial \mathcal W(x)$
denotes the union of the boundaries of the tiles of
$\partial \mathcal W(x)$
denotes the union of the boundaries of the tiles of
![]() $\mathcal W$
. Note that, in this case, the origin
$\mathcal W$
. Note that, in this case, the origin
![]() $0\in \mathbb R^d$
is an interior point of a (unique) tile of
$0\in \mathbb R^d$
is an interior point of a (unique) tile of
![]() $\mathcal W(x)$
. Denote this tile by
$\mathcal W(x)$
. Denote this tile by
![]() $\mathcal W(x)_0$
, and denote the set of R-interior points by
$\mathcal W(x)_0$
, and denote the set of R-interior points by
![]() $\iota _R(\mathcal W)$
.
$\iota _R(\mathcal W)$
.
Otherwise (if
![]() $\mathrm {dist}(0, \partial \mathcal W(x)) \leq R$
), the point x is said to be an R-boundary point. Denote by
$\mathrm {dist}(0, \partial \mathcal W(x)) \leq R$
), the point x is said to be an R-boundary point. Denote by
![]() $\beta _R(\mathcal W)$
the set of R-boundary points.
$\beta _R(\mathcal W)$
the set of R-boundary points.
Note that
![]() $\beta _R(\mathcal W)$
is closed and
$\beta _R(\mathcal W)$
is closed and
![]() $\iota _R(\mathcal W)$
is open.
$\iota _R(\mathcal W)$
is open.
Lemma 3.7. Let
![]() $(X, T, \mathbb Z^d)$
be a dynamical system with the marker property.
$(X, T, \mathbb Z^d)$
be a dynamical system with the marker property.
Fix
![]() $1< s < 2$
. Let
$1< s < 2$
. Let
![]() $R_0> 0$
and
$R_0> 0$
and
![]() $\varepsilon>0$
be arbitrary. Let
$\varepsilon>0$
be arbitrary. Let
![]() $N>N_0$
, where
$N>N_0$
, where
![]() $N_0$
is the constant of Lemma 3.5 with respect to
$N_0$
is the constant of Lemma 3.5 with respect to
![]() $\varepsilon $
and
$\varepsilon $
and
![]() $2R_0+4+\sqrt {d}/2$
, and let
$2R_0+4+\sqrt {d}/2$
, and let
![]() $R_1> \max \{R_0, N\sqrt {d}\}$
.
$R_1> \max \{R_0, N\sqrt {d}\}$
.
Then the open sets
![]() $U'$
and U in the construction can be chosen to be sufficiently small that M is large enough that there exist a finite open cover
$U'$
and U in the construction can be chosen to be sufficiently small that M is large enough that there exist a finite open cover
and
![]() $n_1, n_2, \ldots , n_K \in \mathbb Z^d$
, such that:
$n_1, n_2, \ldots , n_K \in \mathbb Z^d$
, such that:
-
(1)
 $T^{n_i}(U_i) \subseteq \iota _{R_1}(\mathcal W_H) \subseteq \iota _0(\mathcal W_H)$
,
$T^{n_i}(U_i) \subseteq \iota _{R_1}(\mathcal W_H) \subseteq \iota _0(\mathcal W_H)$
,
 $i=1, 2, \ldots , K$
,
$i=1, 2, \ldots , K$
, -
(2) the open sets
can be rearranged into m families as $$ \begin{align*}T^{n_i}(U_i),\quad i=1, 2, \ldots, K,\end{align*} $$
with
$$ \begin{align*}T^{n_i}(U_i),\quad i=1, 2, \ldots, K,\end{align*} $$
with $$ \begin{align*}\left\{\hspace{-3pt} \begin{array}{l} T^{n_{1}}(U_{1}), \ldots, T^{n_{s_1}}(U_{s_1}), \\ T^{n_{s_1+1}}(U_{s_1+1}), \ldots, T^{n_{s_2}}(U_{s_2}), \\ \cdots \\ T^{n_{s_{m-1}+1}}(U_{s_{m-1}+1}), \ldots, T^{n_{s_m}}(U_{s_m}), \end{array} \right. \end{align*} $$
$$ \begin{align*}\left\{\hspace{-3pt} \begin{array}{l} T^{n_{1}}(U_{1}), \ldots, T^{n_{s_1}}(U_{s_1}), \\ T^{n_{s_1+1}}(U_{s_1+1}), \ldots, T^{n_{s_2}}(U_{s_2}), \\ \cdots \\ T^{n_{s_{m-1}+1}}(U_{s_{m-1}+1}), \ldots, T^{n_{s_m}}(U_{s_m}), \end{array} \right. \end{align*} $$
 $m \leq (\lfloor 2\sqrt {d}\rfloor + 1)^d$
, in such a way that the open sets in each family are mutually disjoint, and
$m \leq (\lfloor 2\sqrt {d}\rfloor + 1)^d$
, in such a way that the open sets in each family are mutually disjoint, and
-
(3) for each
 $x\in \iota _0(\mathcal W_H)$
and each
$x\in \iota _0(\mathcal W_H)$
and each
 $c\in \mathrm {int}(\mathcal W_H(x)_0) \cap \mathbb Z^d$
with
$c\in \mathrm {int}(\mathcal W_H(x)_0) \cap \mathbb Z^d$
with
 $\mathrm {dist}(c, \partial \mathcal W_H)>N\sqrt {d}$
, where
$\mathrm {dist}(c, \partial \mathcal W_H)>N\sqrt {d}$
, where
 $\mathrm {int}(\mathcal W_H(x)_0)$
denotes the set of interior points of the cell
$\mathrm {int}(\mathcal W_H(x)_0)$
denotes the set of interior points of the cell
 $\mathcal W_H(x)_0$
, one has
$\mathcal W_H(x)_0$
, one has  $$ \begin{align*}\frac{1}{N^d} \left\vert\left\{n \in \{0, 1, \ldots, N-1\}^d: T^{c+n}(x) \in \bigcup_{i=1}^K T^{n_i}(U_i)\right\}\right\vert < \varepsilon.\end{align*} $$
$$ \begin{align*}\frac{1}{N^d} \left\vert\left\{n \in \{0, 1, \ldots, N-1\}^d: T^{c+n}(x) \in \bigcup_{i=1}^K T^{n_i}(U_i)\right\}\right\vert < \varepsilon.\end{align*} $$
Proof By Lemma 4.1(4) of [Reference Gutman, Lindenstrauss and Tsukamoto14] (see Lemma 3.3), one can choose M to be sufficiently large that for a fixed
![]() $H>(L+\sqrt {d})^2$
, if
$H>(L+\sqrt {d})^2$
, if
![]() $(a, -sH) \in V(x, n)$
for some
$(a, -sH) \in V(x, n)$
for some
![]() $a\in \mathbb R^d$
, then
$a\in \mathbb R^d$
, then
and
 $$ \begin{align} \left\Vert\frac{a}{s}+\left(1-\frac{1}{s}\right)n - \left(a+ \frac{(s-1)H}{sH+t}(n-a)\right)\right\Vert \leq\frac{4}{L+\sqrt{d}} < 4, \end{align} $$
$$ \begin{align} \left\Vert\frac{a}{s}+\left(1-\frac{1}{s}\right)n - \left(a+ \frac{(s-1)H}{sH+t}(n-a)\right)\right\Vert \leq\frac{4}{L+\sqrt{d}} < 4, \end{align} $$
where
![]() $t = \varphi (T^n(x))^{-1}$
(so that
$t = \varphi (T^n(x))^{-1}$
(so that
![]() $a+ \frac {(s-1)H}{sH+t}(n-a)$
is the H-projective image of a).
$a+ \frac {(s-1)H}{sH+t}(n-a)$
is the H-projective image of a).
For each
![]() $n\in \mathbb Z^d$
, define
$n\in \mathbb Z^d$
, define
Note that
![]() $U_n$
is open. For the same n, pick
$U_n$
is open. For the same n, pick
![]() $h_n\in \mathbb Z^d$
such that
$h_n\in \mathbb Z^d$
such that
For each
![]() $x \in U_n$
, there is
$x \in U_n$
, there is
![]() $a \in \partial W_{sH}(x, n)\subseteq \mathbb R^d$
with
$a \in \partial W_{sH}(x, n)\subseteq \mathbb R^d$
with
By the choice of M (and hence H), one has
Since
by (3.3), one has
which implies
In particular,
![]() $T^{h_n}(x) \in \iota _{R_1}(\mathcal W_H)$
, which implies
$T^{h_n}(x) \in \iota _{R_1}(\mathcal W_H)$
, which implies
and this shows the property (1).
 $$ \begin{align} \left\Vert h_n - \left(a+\frac{(s-1)H}{sH+t}(n-a)\right)\right\Vert < 2R_0+4+\sqrt{d}/2. \end{align} $$
$$ \begin{align} \left\Vert h_n - \left(a+\frac{(s-1)H}{sH+t}(n-a)\right)\right\Vert < 2R_0+4+\sqrt{d}/2. \end{align} $$
Since
![]() $a \in \partial W_{sH}(x, n)$
, this implies that
$a \in \partial W_{sH}(x, n)$
, this implies that
![]() $h_n$
is in the
$h_n$
is in the
![]() $(2R_0+4+\sqrt {d}/2)$
-neighborhood of the the H-projective image of
$(2R_0+4+\sqrt {d}/2)$
-neighborhood of the the H-projective image of
![]() $\partial W_{sH}(x, n)$
(with respect to
$\partial W_{sH}(x, n)$
(with respect to
![]() $(n, t)$
).
$(n, t)$
).
On the other hand, if
![]() $x\in \beta _{R_0}(\mathcal W_{sH})$
, then
$x\in \beta _{R_0}(\mathcal W_{sH})$
, then
![]() $\mathrm {dist}(0, \partial W_{sH}(x, n)) \leq R_0$
for some
$\mathrm {dist}(0, \partial W_{sH}(x, n)) \leq R_0$
for some
![]() $n\in \mathbb Z^d$
with
$n\in \mathbb Z^d$
with
![]() $\mathrm {int}(W_{sH}(x, n)) \neq \varnothing $
, which implies that
$\mathrm {int}(W_{sH}(x, n)) \neq \varnothing $
, which implies that
![]() $x \in U_n$
. Therefore, the collection of sets
$x \in U_n$
. Therefore, the collection of sets
![]() $\{U_n: n\in \mathbb Z^d\}$
forms an open cover of
$\{U_n: n\in \mathbb Z^d\}$
forms an open cover of
![]() $\beta _{R_0}(\mathcal W_{sH})$
. Since
$\beta _{R_0}(\mathcal W_{sH})$
. Since
![]() $\beta _{R_0}(\mathcal W_{sH})$
is a compact set, there is a finite subcover
$\beta _{R_0}(\mathcal W_{sH})$
is a compact set, there is a finite subcover
(In fact,
![]() $\{U_n: \left \Vert n\right \Vert <L+\sqrt {d}+ 2R_0\}$
already covers
$\{U_n: \left \Vert n\right \Vert <L+\sqrt {d}+ 2R_0\}$
already covers
![]() $\beta _{R_0}(\mathcal W_{sH})$
by (5) of Lemma 3.2.)
$\beta _{R_0}(\mathcal W_{sH})$
by (5) of Lemma 3.2.)
Assume that
![]() $n_i$
and
$n_i$
and
![]() $n_j$
satisfy
$n_j$
satisfy
Then there are
![]() $x_i\in U_{n_i}$
and
$x_i\in U_{n_i}$
and
![]() $x_j\in U_{n_j}$
with
$x_j\in U_{n_j}$
with
Since
![]() $x_i \in U_{n_i}$
and
$x_i \in U_{n_i}$
and
![]() $x_j \in U_{n_j}$
, by (3.5), one has
$x_j \in U_{n_j}$
, by (3.5), one has
and
 $$ \begin{align*} B_{R_1}(0) & \subseteq W_{H}(T^{h_{n_j}}(x_j), n_j-h_{n_j})\\ & = W_H(T^{h_{n_i}}(x_i), n_j-h_{n_j}). \end{align*} $$
$$ \begin{align*} B_{R_1}(0) & \subseteq W_{H}(T^{h_{n_j}}(x_j), n_j-h_{n_j})\\ & = W_H(T^{h_{n_i}}(x_i), n_j-h_{n_j}). \end{align*} $$
Therefore,
![]() $n_i-h_{n_i} = n_j-h_{n_j}$
, and so
$n_i-h_{n_i} = n_j-h_{n_j}$
, and so
Together with (3.2) and noting that
![]() $s<2$
, one has
$s<2$
, one has
 $$ \begin{align*} \left\Vert n_i - n_j\right\Vert & = \left\Vert h_{n_j} - h_{n_j}\right\Vert \\ & \leq (1-s^{-1})\left\Vert n_i - n_j\right\Vert + \sqrt{d} \\ & < \left\Vert n_i - n_j\right\Vert/2 + \sqrt{d}, \end{align*} $$
$$ \begin{align*} \left\Vert n_i - n_j\right\Vert & = \left\Vert h_{n_j} - h_{n_j}\right\Vert \\ & \leq (1-s^{-1})\left\Vert n_i - n_j\right\Vert + \sqrt{d} \\ & < \left\Vert n_i - n_j\right\Vert/2 + \sqrt{d}, \end{align*} $$
i.e.,
Note that the set
![]() $\mathbb Z^d$
can be divided into
$\mathbb Z^d$
can be divided into
![]() $(\lfloor 2\sqrt {d}\rfloor +1)^d$
families
$(\lfloor 2\sqrt {d}\rfloor +1)^d$
families
![]() $(\mathbb Z^d)_1$
, …,
$(\mathbb Z^d)_1$
, …,
![]() $(\mathbb Z^d)_{(\lfloor 2\sqrt {d}\rfloor + 1)^d}$
such that any pair of elements inside each family has distance between them at least
$(\mathbb Z^d)_{(\lfloor 2\sqrt {d}\rfloor + 1)^d}$
such that any pair of elements inside each family has distance between them at least
![]() $2\sqrt {d}$
, and therefore, by (3.7),
$2\sqrt {d}$
, and therefore, by (3.7),
Then the rearrangement of
![]() $U_{n_1}, \ldots , U_{n_K}$
as
$U_{n_1}, \ldots , U_{n_K}$
as
possesses the property (2).
Let
![]() $x\in \iota _0(\mathcal W_H)$
(then
$x\in \iota _0(\mathcal W_H)$
(then
![]() $\mathcal W_H(x)_0$
is well defined). Write
$\mathcal W_H(x)_0$
is well defined). Write
Assume, there is
![]() $m \in \mathrm {int}(\mathcal W_H(x)_0) \cap \mathbb Z^d$
such that
$m \in \mathrm {int}(\mathcal W_H(x)_0) \cap \mathbb Z^d$
such that
for some
![]() $n_k$
,
$n_k$
,
![]() $k=1, 2, \ldots , K$
.
$k=1, 2, \ldots , K$
.
Since
![]() $m \in \mathrm {int}(\mathcal W_H(x)_0) \cap \mathbb Z^d$
, one has
$m \in \mathrm {int}(\mathcal W_H(x)_0) \cap \mathbb Z^d$
, one has
Hence,
![]() $T^m(x) \in \iota _0(\mathcal W_H)$
and
$T^m(x) \in \iota _0(\mathcal W_H)$
and
By the assumption (3.8), there is
![]() $x_{n_k} \in U_{n_k}$
such that
$x_{n_k} \in U_{n_k}$
such that
Then, with (3.5), one has
that is, the tile
![]() $W_H(T^m(x), n_k-h_{n_k})$
contains
$W_H(T^m(x), n_k-h_{n_k})$
contains
![]() $0$
as an interior point. By (3.9), the tile
$0$
as an interior point. By (3.9), the tile
![]() $W_H(T^m(x), n(x)-m)$
contains
$W_H(T^m(x), n(x)-m)$
contains
![]() $0$
as an interior point, and therefore, these two tiles are same, i.e.,
$0$
as an interior point, and therefore, these two tiles are same, i.e.,
and hence,
Therefore, at the
![]() $-sH$
level, one also has
$-sH$
level, one also has
By (3.6),
![]() $h_{n_k}$
is in the
$h_{n_k}$
is in the
![]() $(2R_0+4+\sqrt {d}/2)$
-neighborhood of the H-projective image of
$(2R_0+4+\sqrt {d}/2)$
-neighborhood of the H-projective image of
![]() $\partial W_{sH}(x_{n_k}, n_k)$
(see Definition 3.4), and therefore,
$\partial W_{sH}(x_{n_k}, n_k)$
(see Definition 3.4), and therefore,
![]() $0$
is in the
$0$
is in the
![]() $(2R_0+4+\sqrt {d}/2)$
-neighborhood of the H-projective image of
$(2R_0+4+\sqrt {d}/2)$
-neighborhood of the H-projective image of
Thus, by (3.10), the origin
![]() $0$
is in the
$0$
is in the
![]() $(2R_0+4+\sqrt {d}/2)$
-neighborhood of the H-projective image of
$(2R_0+4+\sqrt {d}/2)$
-neighborhood of the H-projective image of
![]() $\partial W_{sH}(T^m(x), n(x)-m)$
, and hence, m is in the
$\partial W_{sH}(T^m(x), n(x)-m)$
, and hence, m is in the
![]() $(2R_0+4+\sqrt {d}/2)$
-neighborhood of the H-projective image of
$(2R_0+4+\sqrt {d}/2)$
-neighborhood of the H-projective image of
![]() $\partial W_{sH}(x, n(x))$
, which is denoted by
$\partial W_{sH}(x, n(x))$
, which is denoted by
![]() $\partial W_{sH}^H(x, n(x))$
, i.e.,
$\partial W_{sH}^H(x, n(x))$
, i.e.,
 $$ \begin{align*}\partial W_{sH}^H(x, n(x)):=\left\{a+\frac{(s-1)H}{sH+t}(n(x)-a): a \in \partial W_{sH}(x, n(x))\right\},\end{align*} $$
$$ \begin{align*}\partial W_{sH}^H(x, n(x)):=\left\{a+\frac{(s-1)H}{sH+t}(n(x)-a): a \in \partial W_{sH}(x, n(x))\right\},\end{align*} $$
where
![]() $t= \varphi (T^n(x))^{-1}$
(see Definition 3.4).
$t= \varphi (T^n(x))^{-1}$
(see Definition 3.4).
Therefore, for any
![]() $c\in \mathrm {int}(\mathcal W_H(x)_0) \cap \mathbb Z^d$
with
$c\in \mathrm {int}(\mathcal W_H(x)_0) \cap \mathbb Z^d$
with
![]() $\mathrm {dist}(c, \partial \mathcal W_H)>N\sqrt {d}$
, since
$\mathrm {dist}(c, \partial \mathcal W_H)>N\sqrt {d}$
, since
one has
 $$ \begin{align*} &\quad \left\{ n \in \{0, 1, \ldots, N-1\}^d: T^{c+n}(x) \in \bigcup_{i=1}^K h_i(U_i) \right\} \\ & \subseteq \left\{n \in \{0, 1, \ldots, N-1\}^d: \mathrm{dist}(c+n, \partial W_{sH}^H(x, n(x))) < 2R_0+4+\sqrt{d}/2 \right\}. \end{align*} $$
$$ \begin{align*} &\quad \left\{ n \in \{0, 1, \ldots, N-1\}^d: T^{c+n}(x) \in \bigcup_{i=1}^K h_i(U_i) \right\} \\ & \subseteq \left\{n \in \{0, 1, \ldots, N-1\}^d: \mathrm{dist}(c+n, \partial W_{sH}^H(x, n(x))) < 2R_0+4+\sqrt{d}/2 \right\}. \end{align*} $$
Hence, by the choice of N and Lemma 3.5 (applied to the H-projective image of
![]() $W_{sH}(x, n(x))$
),
$W_{sH}(x, n(x))$
),
 $$ \begin{align*} &\quad \frac{1}{N^d} \left\vert\left\{n \in \{0, 1, \ldots, N-1\}^d: T^{c+n}(x) \in \bigcup_{i=1}^K h_i(U_i)\right\}\right\vert \\ & \leq \frac{1}{N^d} \left\vert\left\{n\in c+ \{0, 1, \ldots, N-1\}^d : \mathrm{dist}(n, \partial W_{sH}^H(x, n(x))) < 2R_0+4+\sqrt{d}/2\right\}\right\vert \\ & < \varepsilon. \end{align*} $$
$$ \begin{align*} &\quad \frac{1}{N^d} \left\vert\left\{n \in \{0, 1, \ldots, N-1\}^d: T^{c+n}(x) \in \bigcup_{i=1}^K h_i(U_i)\right\}\right\vert \\ & \leq \frac{1}{N^d} \left\vert\left\{n\in c+ \{0, 1, \ldots, N-1\}^d : \mathrm{dist}(n, \partial W_{sH}^H(x, n(x))) < 2R_0+4+\sqrt{d}/2\right\}\right\vert \\ & < \varepsilon. \end{align*} $$
This proves the property (3).
4 Two towers
4.1 Rokhlin towers
Let
![]() $x \mapsto \mathcal W(x) = \bigcup _{n\in \mathbb Z^d} W(x, n)$
be a map with
$x \mapsto \mathcal W(x) = \bigcup _{n\in \mathbb Z^d} W(x, n)$
be a map with
![]() $\mathcal W(x)$
a tiling of
$\mathcal W(x)$
a tiling of
![]() $\mathbb R^d$
, where
$\mathbb R^d$
, where
![]() $W(x, n)$
is the cell with label n. Assume that the map
$W(x, n)$
is the cell with label n. Assume that the map
![]() $x\mapsto \mathcal W(x)$
is continuous in the sense that for any
$x\mapsto \mathcal W(x)$
is continuous in the sense that for any
![]() $\varepsilon>0$
and any
$\varepsilon>0$
and any
![]() $W(x, n)$
with nonempty interior, if
$W(x, n)$
with nonempty interior, if
![]() $y\in X$
is sufficiently close to x, then the Hausdorff distance between
$y\in X$
is sufficiently close to x, then the Hausdorff distance between
![]() $W(x, n)$
and
$W(x, n)$
and
![]() $W(y, n)$
is less than
$W(y, n)$
is less than
![]() $\varepsilon $
. One also assumes that the map
$\varepsilon $
. One also assumes that the map
![]() $x \mapsto \mathcal W(x)$
is equivariant in the sense that
$x \mapsto \mathcal W(x)$
is equivariant in the sense that
The tiling functions
![]() $\mathcal W_H$
and
$\mathcal W_H$
and
![]() $\mathcal W_{sH}$
constructed in the previous section clearly satisfy the assumptions above. With such a tiling function, one actually can build a Rokhlin tower as follows:
$\mathcal W_{sH}$
constructed in the previous section clearly satisfy the assumptions above. With such a tiling function, one actually can build a Rokhlin tower as follows:
Let
![]() $N\in \mathbb N$
be arbitrary. Put
$N\in \mathbb N$
be arbitrary. Put
where by
![]() $n \equiv 0 {\ (\mathrm {mod}\ N)} $
, one means
$n \equiv 0 {\ (\mathrm {mod}\ N)} $
, one means
![]() $n_i \equiv 0 {\ (\mathrm {mod}\ N)} $
,
$n_i \equiv 0 {\ (\mathrm {mod}\ N)} $
,
![]() $i=1, 2, \ldots , d$
, if
$i=1, 2, \ldots , d$
, if
![]() $n=(n_1, n_2, \ldots , n_d) \in \mathbb Z^d$
. Note that
$n=(n_1, n_2, \ldots , n_d) \in \mathbb Z^d$
. Note that
![]() $\Omega $
is open.
$\Omega $
is open.
Let
![]() $m \in \{0, 1, \ldots , N-1\}^d$
. Pick an arbitrary
$m \in \{0, 1, \ldots , N-1\}^d$
. Pick an arbitrary
![]() $x \in \Omega $
and consider
$x \in \Omega $
and consider
![]() $T^{-m}(x)$
. Note that
$T^{-m}(x)$
. Note that
![]() $0 \in W(x, n)$
for some
$0 \in W(x, n)$
for some
![]() $n \equiv 0 {\ (\mathrm {mod}\ N)} $
and
$n \equiv 0 {\ (\mathrm {mod}\ N)} $
and
![]() $\mathrm {dist}(0, \partial W(x, n))> N\sqrt {d}$
. Since
$\mathrm {dist}(0, \partial W(x, n))> N\sqrt {d}$
. Since
one has
Hence,
where
For the same reason, if one defines
then
Since the sets
are mutually disjoint, it follows from (4.1) that the sets
are mutually disjoint. That is, they form a Rokhlin tower for
![]() $(X, T, \mathbb Z^d)$
.
$(X, T, \mathbb Z^d)$
.
On the other hand, by (4.2) and the construction of
![]() $\Omega _m"$
, one has
$\Omega _m"$
, one has
In particular, one has
 $$ \begin{align} \mathrm{ocap}\left(X \setminus \bigsqcup_{m \in \{0, 1, \ldots, N-1\}^d} T^{-m}(\Omega)\right) \leq \mathrm{ocap}(\{x \in X: \mathrm{dist}(0, \partial\mathcal W(x)) \leq 2N\sqrt{d}\}). \end{align} $$
$$ \begin{align} \mathrm{ocap}\left(X \setminus \bigsqcup_{m \in \{0, 1, \ldots, N-1\}^d} T^{-m}(\Omega)\right) \leq \mathrm{ocap}(\{x \in X: \mathrm{dist}(0, \partial\mathcal W(x)) \leq 2N\sqrt{d}\}). \end{align} $$
Lemma 4.1. For any
![]() $E>0$
, one has
$E>0$
, one has
where
![]() $\partial _{E+\sqrt {d}}\mathcal W(x) = \{\xi \in \mathbb R^d: \mathrm {dist}(\xi , \partial W(x)) \leq E+\sqrt {d}\}$
.
$\partial _{E+\sqrt {d}}\mathcal W(x) = \{\xi \in \mathbb R^d: \mathrm {dist}(\xi , \partial W(x)) \leq E+\sqrt {d}\}$
.
Proof Pick an arbitrary
![]() $x \in X$
and an arbitrary strictly positive number R, and consider the partial orbit
$x \in X$
and an arbitrary strictly positive number R, and consider the partial orbit
Note that if
![]() $\mathrm {dist}(0, \partial \mathcal W(T^m(x))) \leq E $
(i.e.,
$\mathrm {dist}(0, \partial \mathcal W(T^m(x))) \leq E $
(i.e.,
![]() $0 \in \partial _E\mathcal W(T^m(x))$
) for some m, then
$0 \in \partial _E\mathcal W(T^m(x))$
) for some m, then
Therefore,
One has
 $$ \begin{align*} &\quad \frac{1}{\left\vert B_R \cap \mathbb Z^d\right\vert} \left\vert\{\left\Vert m\right\Vert < R: 0 \in \partial_E\mathcal W(T^m(x))\} \right\vert \\ & \leq \frac{1}{\left\vert B_R \cap \mathbb Z^d\right\vert} \left\vert\{\left\Vert m\right\Vert < R: m \in \partial_E\mathcal W(x)\} \right\vert \\ & \leq \frac{1}{\left\vert B_R \cap \mathbb Z^d\right\vert} \mathrm{vol}(\partial_{E+\sqrt{d}}\mathcal W(x) \cap B_{r+\sqrt{d}}). \end{align*} $$
$$ \begin{align*} &\quad \frac{1}{\left\vert B_R \cap \mathbb Z^d\right\vert} \left\vert\{\left\Vert m\right\Vert < R: 0 \in \partial_E\mathcal W(T^m(x))\} \right\vert \\ & \leq \frac{1}{\left\vert B_R \cap \mathbb Z^d\right\vert} \left\vert\{\left\Vert m\right\Vert < R: m \in \partial_E\mathcal W(x)\} \right\vert \\ & \leq \frac{1}{\left\vert B_R \cap \mathbb Z^d\right\vert} \mathrm{vol}(\partial_{E+\sqrt{d}}\mathcal W(x) \cap B_{r+\sqrt{d}}). \end{align*} $$
Since
 $$ \begin{align*}\lim_{R\to\infty}\frac{ \left\vert B_R \cap \mathbb Z^d\right\vert}{\mathrm{vol}(B_{R})} = 1 \quad\mathrm{and}\quad \lim_{R\to\infty}\frac{ \mathrm{vol}(B_{R+\sqrt{d}})}{\mathrm{vol}(B_{R})} = 1,\end{align*} $$
$$ \begin{align*}\lim_{R\to\infty}\frac{ \left\vert B_R \cap \mathbb Z^d\right\vert}{\mathrm{vol}(B_{R})} = 1 \quad\mathrm{and}\quad \lim_{R\to\infty}\frac{ \mathrm{vol}(B_{R+\sqrt{d}})}{\mathrm{vol}(B_{R})} = 1,\end{align*} $$
Since x is arbitrary, this proves the desired conclusion.
Theorem 4.2. Let
![]() $(X, T, \mathbb Z^d)$
be a dynamical system with the marker property. Then, for any
$(X, T, \mathbb Z^d)$
be a dynamical system with the marker property. Then, for any
![]() $\varepsilon>0$
and
$\varepsilon>0$
and
![]() $N \in \mathbb N$
, there is an open set
$N \in \mathbb N$
, there is an open set
![]() $\Omega \subseteq X$
such that the sets
$\Omega \subseteq X$
such that the sets
are mutually disjoint (and hence form a Rokhlin tower), and
 $$ \begin{align*}\mathrm{ocap}\left(X\setminus\bigcup_{n\in \{0, 1, \ldots, N-1\}^d}T^{-n}(\Omega)\right) < \varepsilon.\end{align*} $$
$$ \begin{align*}\mathrm{ocap}\left(X\setminus\bigcup_{n\in \{0, 1, \ldots, N-1\}^d}T^{-n}(\Omega)\right) < \varepsilon.\end{align*} $$
In other words, the system
![]() $(X, T, \mathbb Z^d)$
has the Uniform Rohklin Property (see Definition 2.7 and Lemma 3.2 of [Reference Niu29]).
$(X, T, \mathbb Z^d)$
has the Uniform Rohklin Property (see Definition 2.7 and Lemma 3.2 of [Reference Niu29]).
Proof By Lemma 4.2 of [Reference Gutman, Lindenstrauss and Tsukamoto14], there is an equivariant
![]() $\mathbb R^d$
-tiling
$\mathbb R^d$
-tiling
![]() $x\mapsto \mathcal W(x)$
such that
$x\mapsto \mathcal W(x)$
such that
The conclusion of the theorem follows by (4.4) and Lemma 4.1 (with
![]() $E=2N\sqrt {d}$
).
$E=2N\sqrt {d}$
).
4.2 The two towers
The Rokhlin tower constructed above, in general, does not cover the whole space X. Now, consider the two continuous tiling functions
![]() $\mathcal W_{sH}$
and
$\mathcal W_{sH}$
and
![]() $\mathcal W_{H}$
of Section 3, and the Rokhlin towers
$\mathcal W_{H}$
of Section 3, and the Rokhlin towers
![]() $\mathcal T_0$
and
$\mathcal T_0$
and
![]() $\mathcal T_1$
constructed from them, respectively. It is still possible that
$\mathcal T_1$
constructed from them, respectively. It is still possible that
![]() $\mathcal T_0$
and
$\mathcal T_0$
and
![]() $\mathcal T_1$
together do not cover the whole space X. However, in the following theorem, one can show that the complement of the tower
$\mathcal T_1$
together do not cover the whole space X. However, in the following theorem, one can show that the complement of the tower
![]() $\mathcal T_0$
can be cut into pieces and then each piece can be translated into the tower
$\mathcal T_0$
can be cut into pieces and then each piece can be translated into the tower
![]() $\mathcal T_1$
in such a way that the orders of the overlaps of the translations are bounded by
$\mathcal T_1$
in such a way that the orders of the overlaps of the translations are bounded by
![]() $(\lfloor 2\sqrt {d}\rfloor + 1)^d$
, and the intersections of these translations with each
$(\lfloor 2\sqrt {d}\rfloor + 1)^d$
, and the intersections of these translations with each
![]() $\mathcal T_1$
-orbit are small. This eventually leads to Cuntz comparison of open sets for minimal-free
$\mathcal T_1$
-orbit are small. This eventually leads to Cuntz comparison of open sets for minimal-free
![]() $\mathbb Z^d$
-actions (Theorem 5.5).
$\mathbb Z^d$
-actions (Theorem 5.5).
Theorem 4.3. Consider a dynamical system
![]() $(X, T, \mathbb Z^d)$
with the marker property. Let
$(X, T, \mathbb Z^d)$
with the marker property. Let
![]() $N\in \mathbb N$
and
$N\in \mathbb N$
and
![]() $\varepsilon>0$
be arbitrary. There exist two Rokhlin towers
$\varepsilon>0$
be arbitrary. There exist two Rokhlin towers
with
![]() $N_0, N_1 \geq N$
and
$N_0, N_1 \geq N$
and
![]() $\Omega _0, \Omega _1\subseteq X$
open, an open cover
$\Omega _0, \Omega _1\subseteq X$
open, an open cover
![]() $\{U_1, U_2, \ldots , U_K\}$
of
$\{U_1, U_2, \ldots , U_K\}$
of
![]() $X \setminus \bigcup _{m} T^{-m}(\Omega _{0})$
, and
$X \setminus \bigcup _{m} T^{-m}(\Omega _{0})$
, and
![]() $h_1, h_2, \ldots , h_K \in \mathbb Z^d$
such that:
$h_1, h_2, \ldots , h_K \in \mathbb Z^d$
such that:
-
(1)
 $T^{h_k}(U_k) \subseteq \bigcup _{m} T^{-m}(\Omega _{1})$
,
$T^{h_k}(U_k) \subseteq \bigcup _{m} T^{-m}(\Omega _{1})$
,
 $k=1, 2, \ldots , K$
;
$k=1, 2, \ldots , K$
; -
(2) the open sets
can be rearranged into m families as $$ \begin{align*}T^{h_k}(U_k),\quad k=1, 2, \ldots, K,\end{align*} $$
for some
$$ \begin{align*}T^{h_k}(U_k),\quad k=1, 2, \ldots, K,\end{align*} $$
for some $$ \begin{align*}\left\{ \begin{array}{l} T^{h_{1}}(U_{1}), \ldots, T^{h_{s_1}}(U_{s_1}), \\ T^{h_{s_1+1}}(U_{s_1+1}), \ldots, T^{h_{s_2}}(U_{s_2}), \\ \cdots \\ T^{h_{s_{m-1}+1}}(U_{s_{m-1}+1}), \ldots, T^{h_{s_m}}(U_{s_m}), \end{array} \right. \end{align*} $$
$$ \begin{align*}\left\{ \begin{array}{l} T^{h_{1}}(U_{1}), \ldots, T^{h_{s_1}}(U_{s_1}), \\ T^{h_{s_1+1}}(U_{s_1+1}), \ldots, T^{h_{s_2}}(U_{s_2}), \\ \cdots \\ T^{h_{s_{m-1}+1}}(U_{s_{m-1}+1}), \ldots, T^{h_{s_m}}(U_{s_m}), \end{array} \right. \end{align*} $$
 $m \leq (\lfloor 2\sqrt {d}\rfloor + 1)^d$
, such that the open sets in each family are mutually disjoint;
$m \leq (\lfloor 2\sqrt {d}\rfloor + 1)^d$
, such that the open sets in each family are mutually disjoint;
-
(3) for each
 $x\in \Omega _{1}$
, one has
$x\in \Omega _{1}$
, one has  $$ \begin{align*}\frac{1}{N_1^d} \left\vert\left\{m \in \{0, 1, \ldots, N_1-1\}^d: T^m(x) \in \bigcup_{k=1}^K T^{n_k}(U_{k})\right\}\right\vert < \varepsilon.\end{align*} $$
$$ \begin{align*}\frac{1}{N_1^d} \left\vert\left\{m \in \{0, 1, \ldots, N_1-1\}^d: T^m(x) \in \bigcup_{k=1}^K T^{n_k}(U_{k})\right\}\right\vert < \varepsilon.\end{align*} $$
Proof Applying Lemma 3.7 with
![]() $R_0 = 2N\sqrt {d}$
,
$R_0 = 2N\sqrt {d}$
,
![]() $\varepsilon $
, and some
$\varepsilon $
, and some
![]() $1< s < 2$
, together with some
$1< s < 2$
, together with some
![]() $N_1>\max \{N(R_0, \varepsilon ), N\}$
(in place of N) and
$N_1>\max \{N(R_0, \varepsilon ), N\}$
(in place of N) and
![]() $R_1> \max \{R_0, 2N_1\sqrt {d}\}$
, where
$R_1> \max \{R_0, 2N_1\sqrt {d}\}$
, where
![]() $N(R_0, \varepsilon )$
is the constant of Lemma 3.5 with respect to
$N(R_0, \varepsilon )$
is the constant of Lemma 3.5 with respect to
![]() $\varepsilon $
and
$\varepsilon $
and
![]() $2R_0+4+\sqrt {d}/2$
(so
$2R_0+4+\sqrt {d}/2$
(so
![]() $N(R_0, \varepsilon )$
is the constant
$N(R_0, \varepsilon )$
is the constant
![]() $N_0$
of Lemma 3.7; but
$N_0$
of Lemma 3.7; but
![]() $N_0$
will be reserved for the height of the first Rokhlin tower in this proof), we obtain two continuous equivariant
$N_0$
will be reserved for the height of the first Rokhlin tower in this proof), we obtain two continuous equivariant
![]() $\mathbb R^d$
-tilings
$\mathbb R^d$
-tilings
![]() $\mathcal W_{sH}$
and
$\mathcal W_{sH}$
and
![]() $\mathcal W_H$
for some (sufficiently large)
$\mathcal W_H$
for some (sufficiently large)
![]() $H>0$
, a finite open cover
$H>0$
, a finite open cover
and
![]() $n_1, n_2, \ldots , n_K \in \mathbb Z^d$
such that:
$n_1, n_2, \ldots , n_K \in \mathbb Z^d$
such that:
-
(1)
 $T^{n_i}(U_i) \subseteq \iota _{R_1}(\mathcal W_H) \subseteq \iota _0(\mathcal W_H)$
,
$T^{n_i}(U_i) \subseteq \iota _{R_1}(\mathcal W_H) \subseteq \iota _0(\mathcal W_H)$
,
 $i=1, 2, \ldots , K$
;
$i=1, 2, \ldots , K$
; -
(2) the open sets
can be rearranged as $$ \begin{align*}T^{n_i}(U_i),\quad i=1, 2, \ldots, K,\end{align*} $$
with
$$ \begin{align*}T^{n_i}(U_i),\quad i=1, 2, \ldots, K,\end{align*} $$
with $$ \begin{align*}\left\{\begin{array}{l} T^{n_{1}}(U_{1}), \ldots, T^{n_{s_1}}(U_{s_1}), \\ T^{n_{s_1+1}}(U_{s_1+1}), \ldots, T^{n_{s_2}}(U_{s_2}), \\ \cdots \\ T^{n_{s_{m-1}+1}}(U_{s_{m-1}+1}), \ldots, T^{n_{s_m}}(U_{s_m}), \end{array} \right. \end{align*} $$
$$ \begin{align*}\left\{\begin{array}{l} T^{n_{1}}(U_{1}), \ldots, T^{n_{s_1}}(U_{s_1}), \\ T^{n_{s_1+1}}(U_{s_1+1}), \ldots, T^{n_{s_2}}(U_{s_2}), \\ \cdots \\ T^{n_{s_{m-1}+1}}(U_{s_{m-1}+1}), \ldots, T^{n_{s_m}}(U_{s_m}), \end{array} \right. \end{align*} $$
 $m \leq (\lfloor 2\sqrt {d}\rfloor + 1)^d$
, such that the open sets in each family are mutually disjoint;
$m \leq (\lfloor 2\sqrt {d}\rfloor + 1)^d$
, such that the open sets in each family are mutually disjoint;
-
(3) for each
 $x\in \iota _0(\mathcal W_H)$
and each
$x\in \iota _0(\mathcal W_H)$
and each
 $c\in \mathrm {int}(\mathcal W_H(x)_0) \cap \mathbb Z^d$
with
$c\in \mathrm {int}(\mathcal W_H(x)_0) \cap \mathbb Z^d$
with
 $\mathrm {dist}(c, \partial \mathcal W_H)>N_1\sqrt {d}$
, one has
$\mathrm {dist}(c, \partial \mathcal W_H)>N_1\sqrt {d}$
, one has  $$ \begin{align*}\frac{1}{N_1^d} \left\vert\left\{n \in \{0, 1, \ldots, N_1-1\}^d: T^{c+n}(x) \in \bigcup_{i=1}^K T^{n_i}(U_i)\right\}\right\vert < \varepsilon.\end{align*} $$
$$ \begin{align*}\frac{1}{N_1^d} \left\vert\left\{n \in \{0, 1, \ldots, N_1-1\}^d: T^{c+n}(x) \in \bigcup_{i=1}^K T^{n_i}(U_i)\right\}\right\vert < \varepsilon.\end{align*} $$
Put
Then the sets
form a Rokhlin tower with
![]() $N_0=N$
, and by (4.3),
$N_0=N$
, and by (4.3),
Thus,
![]() $U_1, U_2, \ldots , U_K$
form an open cover of
$U_1, U_2, \ldots , U_K$
form an open cover of
![]() $X\setminus \bigsqcup _{m \in \{0, 1, \ldots , N_0-1\}^d} T^{-m}(\Omega _0)$
.
$X\setminus \bigsqcup _{m \in \{0, 1, \ldots , N_0-1\}^d} T^{-m}(\Omega _0)$
.
Put
Then the sets
form a Rokhlin tower, and by (4.3) (and the assumption that
![]() $R_1> 2N_1\sqrt {d}$
),
$R_1> 2N_1\sqrt {d}$
),
Thus,
![]() $T^{-h_i}(U_i) \subseteq \bigsqcup _{m \in \{0, 1, \ldots , N_1-1\}^d} T^{-m}(\Omega _1)$
.
$T^{-h_i}(U_i) \subseteq \bigsqcup _{m \in \{0, 1, \ldots , N_1-1\}^d} T^{-m}(\Omega _1)$
.
If
![]() $x\in \Omega _1$
(whence
$x\in \Omega _1$
(whence
![]() $x\in \iota _0(\mathcal W_H)$
and
$x\in \iota _0(\mathcal W_H)$
and
![]() $\mathrm {dist}(0, \partial \mathcal W_H)>N_1\sqrt {d}$
), it then follows from (3) (with
$\mathrm {dist}(0, \partial \mathcal W_H)>N_1\sqrt {d}$
), it then follows from (3) (with
![]() $c=0$
) that
$c=0$
) that
 $$ \begin{align*}\frac{1}{N_1^d} \left\vert\left\{m \in \{0, 1, \ldots, N_1-1\}^d: T^m(x) \in \bigcup_{k=1}^K T^{n_k}(U_{k})\right\}\right\vert < \varepsilon,\end{align*} $$
$$ \begin{align*}\frac{1}{N_1^d} \left\vert\left\{m \in \{0, 1, \ldots, N_1-1\}^d: T^m(x) \in \bigcup_{k=1}^K T^{n_k}(U_{k})\right\}\right\vert < \varepsilon,\end{align*} $$
as desired.
5 Cuntz comparison of open sets, radius of comparison, and the mean topological dimension
With the two-tower construction in the previous section, let us show that the C*-algebra
![]() $\mathrm {C}(X)\rtimes \mathbb Z^d$
has Cuntz comparison of open sets (Theorem 5.5), and therefore, the radius of comparison of
$\mathrm {C}(X)\rtimes \mathbb Z^d$
has Cuntz comparison of open sets (Theorem 5.5), and therefore, the radius of comparison of
![]() $\mathrm {C}(X)\rtimes \mathbb Z^d$
is at most half of the mean dimension of
$\mathrm {C}(X)\rtimes \mathbb Z^d$
is at most half of the mean dimension of
![]() $(X, T, \mathbb Z^d)$
.
$(X, T, \mathbb Z^d)$
.
As a preparation, one has the following two simple observations on the Cuntz semigroup of a C*-algebra.
Lemma 5.1. Let A be a C*-algebra, and let
![]() $a_1, a_2, \ldots , a_m \in A$
be positive elements. Then
$a_1, a_2, \ldots , a_m \in A$
be positive elements. Then
Proof The lemma follows from the observation:
 $$ \begin{align*}\left( \begin{array}{cccc} a_1 & & & \\ & a_2 & & \\ & & \ddots & \\ & & & a_m \end{array} \right) \leq \left( \begin{array}{cccc} a_1+\cdots+a_m & & & \\ & a_1+\cdots+a_m & & \\ & & \ddots & \\ & & & a_1+\cdots + a_m \end{array} \right). \end{align*} $$
$$ \begin{align*}\left( \begin{array}{cccc} a_1 & & & \\ & a_2 & & \\ & & \ddots & \\ & & & a_m \end{array} \right) \leq \left( \begin{array}{cccc} a_1+\cdots+a_m & & & \\ & a_1+\cdots+a_m & & \\ & & \ddots & \\ & & & a_1+\cdots + a_m \end{array} \right). \end{align*} $$
For any open set
![]() $U\subseteq X$
, recall that
$U\subseteq X$
, recall that
![]() $\varphi _U$
is a positive continuous function on X such that
$\varphi _U$
is a positive continuous function on X such that
![]() $U = \varphi ^{-1}_U(0, +\infty )$
(see Example 2.9).
$U = \varphi ^{-1}_U(0, +\infty )$
(see Example 2.9).
Lemma 5.2. Let
![]() $U_1, U_2, \ldots , U_K \subseteq X$
be open sets which can be divided into M families in such a way that each family consists of mutually disjoint sets. Then
$U_1, U_2, \ldots , U_K \subseteq X$
be open sets which can be divided into M families in such a way that each family consists of mutually disjoint sets. Then
Proof Write
![]() $U_1, U_2, \ldots , U_K$
as
$U_1, U_2, \ldots , U_K$
as
so that the open sets in each family are mutually disjoint. Then
and together with the lemma above, one has
 $$ \begin{align*} [\varphi_{U_1}] + \cdots + [\varphi_{U_K}] & = [\varphi_{U_{1}} + \cdots + \varphi_{U_{s_1}}] + \cdots + [\varphi_{U_{s_{m-1}+1}} + \cdots + \varphi_{U_{s_M}}] \\ &= [\varphi_{U_{1} \cup\cdots\cup U_{s_1}}] + \cdots + [\varphi_{U_{s_{m-1}+1} \cup \cdots \cup U_{s_M}}] \\ & \leq M [\varphi_{U_1\cup\cdots\cup U_K}], \end{align*} $$
$$ \begin{align*} [\varphi_{U_1}] + \cdots + [\varphi_{U_K}] & = [\varphi_{U_{1}} + \cdots + \varphi_{U_{s_1}}] + \cdots + [\varphi_{U_{s_{m-1}+1}} + \cdots + \varphi_{U_{s_M}}] \\ &= [\varphi_{U_{1} \cup\cdots\cup U_{s_1}}] + \cdots + [\varphi_{U_{s_{m-1}+1} \cup \cdots \cup U_{s_M}}] \\ & \leq M [\varphi_{U_1\cup\cdots\cup U_K}], \end{align*} $$
as desired.
Definition 5.3. Consider a topological dynamical system
![]() $(X, \Gamma )$
, where X is a compact metrizable space and
$(X, \Gamma )$
, where X is a compact metrizable space and
![]() $\Gamma $
is a discrete group acting on X on the right, and consider a Rokhlin tower
$\Gamma $
is a discrete group acting on X on the right, and consider a Rokhlin tower
where
![]() $\Omega \subseteq X$
is open and
$\Omega \subseteq X$
is open and
![]() $\Gamma _0\subseteq \Gamma $
is a finite set containing the unit e of the discrete group
$\Gamma _0\subseteq \Gamma $
is a finite set containing the unit e of the discrete group
![]() $\Gamma $
. Define the C*-algebra
$\Gamma $
. Define the C*-algebra
By Lemma 3.11 of [Reference Niu29],
![]() $\textrm {C*}(\mathcal T)$
is canonically isomorphic to
$\textrm {C*}(\mathcal T)$
is canonically isomorphic to
![]() $\mathrm {M}_{\left \vert \Gamma _0\right \vert }(\mathrm {C}_0(\Omega ))$
, and
$\mathrm {M}_{\left \vert \Gamma _0\right \vert }(\mathrm {C}_0(\Omega ))$
, and
under this isomorphism.
The following comparison result is essentially a special case of Theorem 7.8 of [Reference Niu29].
Lemma 5.4. (Theorem 7.8 of [Reference Niu29])
Let Z be a locally compact metrizable space, and consider the C*-algebra
![]() $\mathrm {M}_n(\mathrm {C}_0(Z))$
. Let
$\mathrm {M}_n(\mathrm {C}_0(Z))$
. Let
![]() $a, b \in \mathrm {M}_n(\mathrm {C}_0(Z))$
be two positive diagonal elements, i.e.,
$a, b \in \mathrm {M}_n(\mathrm {C}_0(Z))$
be two positive diagonal elements, i.e.,
for continuous functions
![]() $a_1, \ldots , a_n, b_1, \ldots , b_n: Z \to [0, +\infty )$
. If
$a_1, \ldots , a_n, b_1, \ldots , b_n: Z \to [0, +\infty )$
. If
and
then
![]() $a \precsim b$
in
$a \precsim b$
in
![]() $\mathrm {M}_n(\mathrm {C}_0(Z))$
.
$\mathrm {M}_n(\mathrm {C}_0(Z))$
.
Proof It is enough to show that
![]() $(a-\varepsilon )_+ \precsim b$
for arbitrary
$(a-\varepsilon )_+ \precsim b$
for arbitrary
![]() $\varepsilon>0$
. For a given
$\varepsilon>0$
. For a given
![]() $\varepsilon>0$
, there is a compact subset
$\varepsilon>0$
, there is a compact subset
![]() $D \subseteq Z$
such that
$D \subseteq Z$
such that
![]() $(a-\varepsilon )_+$
is supported inside D. Denote by
$(a-\varepsilon )_+$
is supported inside D. Denote by
![]() $\pi : \mathrm {M}_n(\mathrm {C}_0(Z)) \to \mathrm {M}_{n}(\mathrm {C}(D))$
the restriction map. One then has
$\pi : \mathrm {M}_n(\mathrm {C}_0(Z)) \to \mathrm {M}_{n}(\mathrm {C}(D))$
the restriction map. One then has
and
By Theorem 7.8 of [Reference Niu29], one has
![]() $\pi ((a-\varepsilon )_+) \precsim \pi (b)$
in
$\pi ((a-\varepsilon )_+) \precsim \pi (b)$
in
![]() $\mathrm {M}_n(\mathrm {C}(D))$
, i.e., there is a sequence
$\mathrm {M}_n(\mathrm {C}(D))$
, i.e., there is a sequence
![]() $(v_k) \subseteq \mathrm {M}_n(\mathrm {C}(D))$
such that
$(v_k) \subseteq \mathrm {M}_n(\mathrm {C}(D))$
such that
![]() $v_k(\pi (b))v_k^* \to \pi ((a-\varepsilon )_+)$
as
$v_k(\pi (b))v_k^* \to \pi ((a-\varepsilon )_+)$
as
![]() $k \to \infty $
. Extend each
$k \to \infty $
. Extend each
![]() $v_k$
to a function in
$v_k$
to a function in
![]() $\mathrm {M}_n(\mathrm {C}_0(Z))$
, and still denote it by
$\mathrm {M}_n(\mathrm {C}_0(Z))$
, and still denote it by
![]() $v_k$
. It is clear that the new sequence
$v_k$
. It is clear that the new sequence
![]() $(v_k)$
satisfies
$(v_k)$
satisfies
![]() $v_kbv_k^* \to (a-\varepsilon )_+$
as
$v_kbv_k^* \to (a-\varepsilon )_+$
as
![]() $k\to \infty $
, and hence
$k\to \infty $
, and hence
![]() $(a - \varepsilon )_+ \precsim b$
, as desired.
$(a - \varepsilon )_+ \precsim b$
, as desired.
Theorem 5.5. Let
![]() $(X, T, \mathbb Z^d)$
be a dynamical system with the marker property, and let
$(X, T, \mathbb Z^d)$
be a dynamical system with the marker property, and let
![]() $E, F\subseteq X$
be open sets such that
$E, F\subseteq X$
be open sets such that
Then,
in the Cuntz semigroup of
![]() $\mathrm {C}(X) \rtimes \mathbb Z^d$
, where
$\mathrm {C}(X) \rtimes \mathbb Z^d$
, where
![]() $\varphi _E$
and
$\varphi _E$
and
![]() $\varphi _F$
are continuous functions supported on E and F, respectively (see Example 2.9). In other words, the C*-algebra
$\varphi _F$
are continuous functions supported on E and F, respectively (see Example 2.9). In other words, the C*-algebra
![]() $\mathrm {C}(X) \rtimes \mathbb Z^d$
has
$\mathrm {C}(X) \rtimes \mathbb Z^d$
has
![]() $(\frac {1}{4}, (2\lfloor \sqrt {d}\rfloor + 1)^d + 1)$
-COS (see Definition 2.11).
$(\frac {1}{4}, (2\lfloor \sqrt {d}\rfloor + 1)^d + 1)$
-COS (see Definition 2.11).
Proof Let E and F be open sets satisfying the condition of the theorem. Let
![]() $\varepsilon>0$
be arbitrary. In order to prove the statement of the theorem, it is enough to show that
$\varepsilon>0$
be arbitrary. In order to prove the statement of the theorem, it is enough to show that
 $$ \begin{align*}(\varphi_E - \varepsilon)_+ \precsim \underbrace{\varphi_F \oplus\cdots\oplus \varphi_F}_{(2\lfloor\sqrt{d}\rfloor + 1)^d + 1}.\end{align*} $$
$$ \begin{align*}(\varphi_E - \varepsilon)_+ \precsim \underbrace{\varphi_F \oplus\cdots\oplus \varphi_F}_{(2\lfloor\sqrt{d}\rfloor + 1)^d + 1}.\end{align*} $$
For the given
![]() $\varepsilon $
, pick a compact set
$\varepsilon $
, pick a compact set
![]() $E'\subseteq E$
such that
$E'\subseteq E$
such that
By the assumption of the theorem, one has
It follows that there is
![]() $N\in \mathbb N$
such that for any
$N\in \mathbb N$
such that for any
![]() $M> N$
and any
$M> N$
and any
![]() $x\in X$
,
$x\in X$
,
Otherwise, there are sequences
![]() $N_k\in \mathbb N$
,
$N_k\in \mathbb N$
,
![]() $x_k\in X$
,
$x_k\in X$
,
![]() $k=1, 2, \ldots , $
such that
$k=1, 2, \ldots , $
such that
![]() $N_k\to \infty $
as
$N_k\to \infty $
as
![]() $k\to \infty $
, and for any k,
$k\to \infty $
, and for any k,
 $$ \begin{align*}\frac{1}{N_k^d}\{m \in \{0, 1, \ldots, N_k-1\}^d: T^{-m}(x_k) \in E'\} \geq \frac{1}{4} \frac{1}{N_k^d}\{m \in \{0, 1, \ldots, N_k-1\}^d: T^{-m}(x_k) \in F\}.\end{align*} $$
$$ \begin{align*}\frac{1}{N_k^d}\{m \in \{0, 1, \ldots, N_k-1\}^d: T^{-m}(x_k) \in E'\} \geq \frac{1}{4} \frac{1}{N_k^d}\{m \in \{0, 1, \ldots, N_k-1\}^d: T^{-m}(x_k) \in F\}.\end{align*} $$
That is,
where
![]() $\delta _{N_k, x_k}=\frac {1}{N_k^d}\sum _{m\in \{0, 1, \ldots , N_k-1\}^d}\delta _{T^{-m}(x_k)}$
and
$\delta _{N_k, x_k}=\frac {1}{N_k^d}\sum _{m\in \{0, 1, \ldots , N_k-1\}^d}\delta _{T^{-m}(x_k)}$
and
![]() $\delta _y$
is the Dirac measure concentrated at y. Let
$\delta _y$
is the Dirac measure concentrated at y. Let
![]() $\delta _\infty $
be a limit point of
$\delta _\infty $
be a limit point of
![]() $\{\delta _{N_k, x_k}, k=1, 2, \ldots \}$
. It is clear that
$\{\delta _{N_k, x_k}, k=1, 2, \ldots \}$
. It is clear that
![]() $\delta _\infty \in \mathcal M_1(X, T, \mathbb Z^d)$
. Passing to a subsequence of k, one has
$\delta _\infty \in \mathcal M_1(X, T, \mathbb Z^d)$
. Passing to a subsequence of k, one has
 $$ \begin{align*} \delta_\infty(F) &\leq \liminf_{k\to\infty} \delta_{N_k, x_k}(F)\quad\quad\quad (F\textrm{ is open)} \\ & \leq 4 \liminf_{k\to\infty} \delta_{N_k, x_k}(E')\quad\quad\quad (\textrm{by}\ (5.4))\\ & \leq 4 \limsup_{k\to\infty} \delta_{N_k, x_k}(E') \\ & \leq 4 \delta_\infty(E') \quad\quad\quad (E' \textrm{ is closed}), \end{align*} $$
$$ \begin{align*} \delta_\infty(F) &\leq \liminf_{k\to\infty} \delta_{N_k, x_k}(F)\quad\quad\quad (F\textrm{ is open)} \\ & \leq 4 \liminf_{k\to\infty} \delta_{N_k, x_k}(E')\quad\quad\quad (\textrm{by}\ (5.4))\\ & \leq 4 \limsup_{k\to\infty} \delta_{N_k, x_k}(E') \\ & \leq 4 \delta_\infty(E') \quad\quad\quad (E' \textrm{ is closed}), \end{align*} $$
which contradicts (5.2).
By (5.1) and (5.3), for any
![]() $M> N$
and any
$M> N$
and any
![]() $x\in X$
,
$x\in X$
,
 $$ \begin{align} & \frac{1}{M^d}\{m\in \{0, 1, \ldots, M-1\}^d: (\varphi_E-\varepsilon)_+(T^{-m}(x))> 0\} \\ &\leq \frac{1}{M^d}\{m \in \{0, 1, \ldots, M-1\}^d: T^{-m}(x) \in E'\}\nonumber \\ &< \frac{1}{4} \frac{1}{M^d}\{m \in \{0, 1, \ldots, M-1\}^d: T^{-m}(x) \in F\} \nonumber \\ & = \frac{1}{4}\frac{1}{M^d}\{m\in \{0, 1, \ldots, M-1\}^d: \varphi_F(T^{-m}(x))> 0\}. \nonumber \end{align} $$
$$ \begin{align} & \frac{1}{M^d}\{m\in \{0, 1, \ldots, M-1\}^d: (\varphi_E-\varepsilon)_+(T^{-m}(x))> 0\} \\ &\leq \frac{1}{M^d}\{m \in \{0, 1, \ldots, M-1\}^d: T^{-m}(x) \in E'\}\nonumber \\ &< \frac{1}{4} \frac{1}{M^d}\{m \in \{0, 1, \ldots, M-1\}^d: T^{-m}(x) \in F\} \nonumber \\ & = \frac{1}{4}\frac{1}{M^d}\{m\in \{0, 1, \ldots, M-1\}^d: \varphi_F(T^{-m}(x))> 0\}. \nonumber \end{align} $$
Note that, by the assumption,
The compactness argument same as above shows that N can be chosen sufficiently large so that there is
![]() $\delta>0$
such that for any
$\delta>0$
such that for any
![]() $M>N$
,
$M>N$
,
Let
and
denote the two towers obtained from Theorem 4.3 with respect to
![]() $\max \{N, \sqrt [d]{\frac {1}{\delta }}\}$
and
$\max \{N, \sqrt [d]{\frac {1}{\delta }}\}$
and
![]() $\delta $
. Denote by
$\delta $
. Denote by
![]() $U_1, U_2, \ldots , U_K$
and
$U_1, U_2, \ldots , U_K$
and
![]() $n_1, n_2, \ldots , n_K\in \mathbb Z^d$
, the open sets and group elements, respectively, obtained from Theorem 4.3.
$n_1, n_2, \ldots , n_K\in \mathbb Z^d$
, the open sets and group elements, respectively, obtained from Theorem 4.3.
Pick
![]() $\chi _0 \in \mathrm {C}(X)^+$
such that
$\chi _0 \in \mathrm {C}(X)^+$
such that
 $$ \begin{align} \left\{ \begin{array}{ll} \chi_0(x) = 1, & x\notin \bigcup_{k=1}^K U_k, \\ \chi_0(x)> 0, & x \in \bigsqcup_{m\in \{0, 1, \ldots, N_0-1\}^d} T^{-m}(\Omega_0), \\ \chi_0(x) = 0, & x \notin \bigsqcup_{m\in \{0, 1, \ldots, N_0-1\}^d} T^{-m}(\Omega_0). \end{array} \right. \end{align} $$
$$ \begin{align} \left\{ \begin{array}{ll} \chi_0(x) = 1, & x\notin \bigcup_{k=1}^K U_k, \\ \chi_0(x)> 0, & x \in \bigsqcup_{m\in \{0, 1, \ldots, N_0-1\}^d} T^{-m}(\Omega_0), \\ \chi_0(x) = 0, & x \notin \bigsqcup_{m\in \{0, 1, \ldots, N_0-1\}^d} T^{-m}(\Omega_0). \end{array} \right. \end{align} $$
Note that then
![]() $(1-\chi _0)$
is supported in the set
$(1-\chi _0)$
is supported in the set
![]() $U_1\cup U_2\cup \cdots \cup U_K$
. Consider
$U_1\cup U_2\cup \cdots \cup U_K$
. Consider
Then, for any
![]() $x\in \Omega _0$
, it follows from (5.5) and (5.7) that
$x\in \Omega _0$
, it follows from (5.5) and (5.7) that
 $$ \begin{align*} &\quad \left\vert\{m\in\{0, 1, \ldots, N_0-1\}^d: ((\varphi_{E} - \varepsilon)_+\chi_0)(T^{-m}(x))>0 \} \right\vert\\ & = \left\vert\{m\in\{0, 1, \ldots, N_0-1\}^d: (\varphi_{E} - \varepsilon)_+(T^{-m}(x))>0 \}\right\vert \\ & < \frac{1}{4} \left\vert\{m\in\{0, 1, \ldots, N_0-1\}^d: \varphi_{F}(T^{-m}(x))>0 \} \right\vert \\ & = \frac{1}{4} \left\vert\{m\in\{0, 1, \ldots, N_0-1\}^d: (\varphi_{F}\chi_0)(T^{-m}(x))>0 \}\right\vert. \end{align*} $$
$$ \begin{align*} &\quad \left\vert\{m\in\{0, 1, \ldots, N_0-1\}^d: ((\varphi_{E} - \varepsilon)_+\chi_0)(T^{-m}(x))>0 \} \right\vert\\ & = \left\vert\{m\in\{0, 1, \ldots, N_0-1\}^d: (\varphi_{E} - \varepsilon)_+(T^{-m}(x))>0 \}\right\vert \\ & < \frac{1}{4} \left\vert\{m\in\{0, 1, \ldots, N_0-1\}^d: \varphi_{F}(T^{-m}(x))>0 \} \right\vert \\ & = \frac{1}{4} \left\vert\{m\in\{0, 1, \ldots, N_0-1\}^d: (\varphi_{F}\chi_0)(T^{-m}(x))>0 \}\right\vert. \end{align*} $$
Therefore, with respect to the isomorphism
![]() $\textrm {C*}(\mathcal T_0) \cong \mathrm {M}_{N^d_0}(\mathrm C_0(\Omega _0))$
(see Definition 5.3), one has
$\textrm {C*}(\mathcal T_0) \cong \mathrm {M}_{N^d_0}(\mathrm C_0(\Omega _0))$
(see Definition 5.3), one has
Moreover, it follows from (5.6) and the fact that
![]() $N_0> \sqrt [d]{\frac {1}{\delta }}$
that, for any
$N_0> \sqrt [d]{\frac {1}{\delta }}$
that, for any
![]() $x\in \Omega _0$
,
$x\in \Omega _0$
,
Then, by Lemma 5.4,
Consider the product
![]() $(\varphi _E-\varepsilon )_+(1-\chi _0)$
. Since
$(\varphi _E-\varepsilon )_+(1-\chi _0)$
. Since
![]() $(1-\chi _0)$
is supported in
$(1-\chi _0)$
is supported in
![]() $U_1 \cup U_2 \cup \cdots \cup U_K$
, one has
$U_1 \cup U_2 \cup \cdots \cup U_K$
, one has
On the other hand, by Lemma 5.2,
Note that
![]() $\varphi _{U_i} \sim \varphi _{T^{n_i}(U_i)}$
,
$\varphi _{U_i} \sim \varphi _{T^{n_i}(U_i)}$
,
![]() $i=1, 2, \ldots , K$
, and so one has
$i=1, 2, \ldots , K$
, and so one has
By Theorem 4.3,
 $$ \begin{align} \frac{1}{N_1^d}\left\vert\left\{m \in\{0, 1, \ldots, N_1-1\}^d: T^{-m}(x) \in \bigcup_{k=1}^K T^{n_k}(U_k) \right\}\right\vert < \delta,\quad x\in\Omega_1. \end{align} $$
$$ \begin{align} \frac{1}{N_1^d}\left\vert\left\{m \in\{0, 1, \ldots, N_1-1\}^d: T^{-m}(x) \in \bigcup_{k=1}^K T^{n_k}(U_k) \right\}\right\vert < \delta,\quad x\in\Omega_1. \end{align} $$
Let
![]() $\chi _1: X \to [0, 1]$
be a continuous function such that
$\chi _1: X \to [0, 1]$
be a continuous function such that
 $$ \begin{align*} \left\{ \begin{array}{ll} \chi_1(x)> 0, & x \in \bigsqcup_{m\in \{0, 1, \ldots, N_1-1\}^d} T^{-m}(\Omega_1), \\ \chi_1(x) = 0, & x \notin \bigsqcup_{m\in \{0, 1, \ldots, N_1-1\}^d} T^{-m}(\Omega_1). \end{array} \right. \end{align*} $$
$$ \begin{align*} \left\{ \begin{array}{ll} \chi_1(x)> 0, & x \in \bigsqcup_{m\in \{0, 1, \ldots, N_1-1\}^d} T^{-m}(\Omega_1), \\ \chi_1(x) = 0, & x \notin \bigsqcup_{m\in \{0, 1, \ldots, N_1-1\}^d} T^{-m}(\Omega_1). \end{array} \right. \end{align*} $$
Then
for all
![]() $x\in \Omega _1$
, and hence, by (5.10), one has
$x\in \Omega _1$
, and hence, by (5.10), one has
 $$ \begin{align*} \mathrm{rank}(\varphi_{T^{n_1}(U_1)\cup\cdots\cup T^{n_K}(U_K)}(x)) &= \left\vert\left\{m \in\{0, 1, \ldots, N_1-1\}^d: T^{-m}(x) \in \bigcup_{k=1}^K T^{n_k}(U_k) \right\}\right\vert \\ & < N_1^d\delta < \frac{1}{4}\mathrm{rank}((\varphi_F\chi_1)(x)) \end{align*} $$
$$ \begin{align*} \mathrm{rank}(\varphi_{T^{n_1}(U_1)\cup\cdots\cup T^{n_K}(U_K)}(x)) &= \left\vert\left\{m \in\{0, 1, \ldots, N_1-1\}^d: T^{-m}(x) \in \bigcup_{k=1}^K T^{n_k}(U_k) \right\}\right\vert \\ & < N_1^d\delta < \frac{1}{4}\mathrm{rank}((\varphi_F\chi_1)(x)) \end{align*} $$
for any
![]() $x\in \Omega _1$
.
$x\in \Omega _1$
.
By Lemma 5.4,
and together with (5.9) and (5.8), this implies
 $$ \begin{align*} (\varphi_{E} - \varepsilon)_+ & \precsim (\varphi_{E} - \varepsilon)_+(1- \chi_0) \oplus (\varphi_{E} - \varepsilon)_+ \chi_0 \\ &\precsim (\bigoplus_{(2\lfloor\sqrt{d}\rfloor + 1)^d} (\varphi_{T^{n_1}(U_1)\cup\cdots\cup T^{n_K}(U_K)})) \oplus \varphi_F \\ & \precsim (\bigoplus_{(2\lfloor\sqrt{d}\rfloor + 1)^d} \varphi_F) \oplus \varphi_F, \end{align*} $$
$$ \begin{align*} (\varphi_{E} - \varepsilon)_+ & \precsim (\varphi_{E} - \varepsilon)_+(1- \chi_0) \oplus (\varphi_{E} - \varepsilon)_+ \chi_0 \\ &\precsim (\bigoplus_{(2\lfloor\sqrt{d}\rfloor + 1)^d} (\varphi_{T^{n_1}(U_1)\cup\cdots\cup T^{n_K}(U_K)})) \oplus \varphi_F \\ & \precsim (\bigoplus_{(2\lfloor\sqrt{d}\rfloor + 1)^d} \varphi_F) \oplus \varphi_F, \end{align*} $$
as desired.
Theorem 5.6. Let
![]() $(X, T, \mathbb Z^d)$
be a minimal-free dynamical system. Then
$(X, T, \mathbb Z^d)$
be a minimal-free dynamical system. Then
Proof Note that any minimal-free dynamical system has the marker property. By Theorem 5.5, the C*-algebra
![]() $\mathrm {C}(X) \rtimes \mathbb Z^d$
has the property COS. By Theorem 4.2, the dynamical system
$\mathrm {C}(X) \rtimes \mathbb Z^d$
has the property COS. By Theorem 4.2, the dynamical system
![]() $(X, T, \mathbb Z^d)$
has the property URP. The statement follows directly from Theorem 4.8 of [Reference Niu29].
$(X, T, \mathbb Z^d)$
has the property URP. The statement follows directly from Theorem 4.8 of [Reference Niu29].
Remark 5.7. The proof of Theorem 4.8 of [Reference Niu29] used the simplicity of the C*-algebra
![]() $\mathrm {C}(X)\rtimes \mathbb Z^d$
.
$\mathrm {C}(X)\rtimes \mathbb Z^d$
.
The following corollary generalizes Corollary 4.9 of [Reference Elliott and Niu7] (where
![]() $d=1$
) and generalizes the classifiability result of [Reference Szabó33] (where
$d=1$
) and generalizes the classifiability result of [Reference Szabó33] (where
![]() $\mathrm {dim}(X) < \infty $
).
$\mathrm {dim}(X) < \infty $
).
Theorem 5.8 Let
![]() $(X, T, \mathbb Z^d)$
be a minimal-free dynamical system with mean dimension zero. Then
$(X, T, \mathbb Z^d)$
be a minimal-free dynamical system with mean dimension zero. Then
![]() $\mathrm {C}(X) \rtimes \mathbb Z^d$
absorbs the Jiang–Su algebra tensorially, and hence is classified by its Elliott invariant (i.e., belongs to the classifiable class of Theorem 2.7 of [Reference Elliott, Gong, Lin and Niu4]). In particular, if
$\mathrm {C}(X) \rtimes \mathbb Z^d$
absorbs the Jiang–Su algebra tensorially, and hence is classified by its Elliott invariant (i.e., belongs to the classifiable class of Theorem 2.7 of [Reference Elliott, Gong, Lin and Niu4]). In particular, if
![]() $\mathrm {dim}(X) < \infty $
, or
$\mathrm {dim}(X) < \infty $
, or
![]() $(X, T, \mathbb Z^d)$
has at most countably many ergodic measures, or
$(X, T, \mathbb Z^d)$
has at most countably many ergodic measures, or
![]() $(X, T, \mathbb Z^d)$
has finite topological entropy, then
$(X, T, \mathbb Z^d)$
has finite topological entropy, then
![]() $\mathrm {C}(X) \rtimes \mathbb Z^d$
is classified by its Elliott invariant.
$\mathrm {C}(X) \rtimes \mathbb Z^d$
is classified by its Elliott invariant.
Proof By Theorems 4.2 and 5.5, the dynamical system
![]() $(X, \mathbb Z^d)$
has the URP and COS. The statement then follows from Theorem 4.8 of [Reference Niu28].
$(X, \mathbb Z^d)$
has the URP and COS. The statement then follows from Theorem 4.8 of [Reference Niu28].
The following is a generalization of Corollary 5.7 of [Reference Elliott and Niu7].
Corollary 5.9. Let
![]() $(X_1, T_1, \mathbb Z^{d_1})$
and
$(X_1, T_1, \mathbb Z^{d_1})$
and
![]() $(X_2, T_2, \mathbb Z^{d_2})$
be arbitrary minimal-free dynamical systems, where
$(X_2, T_2, \mathbb Z^{d_2})$
be arbitrary minimal-free dynamical systems, where
![]() $d_1, d_2 \in \mathbb N$
. Then the tensor product C*-algebra
$d_1, d_2 \in \mathbb N$
. Then the tensor product C*-algebra
![]() $(\mathrm {C}(X_1) \rtimes \mathbb Z^{d_1}) \otimes (\mathrm {C}(X_2) \rtimes \mathbb Z^{d_2})$
absorbs the Jiang–Su algebra tensorially, and hence is classified by its Elliott invariant.
$(\mathrm {C}(X_1) \rtimes \mathbb Z^{d_1}) \otimes (\mathrm {C}(X_2) \rtimes \mathbb Z^{d_2})$
absorbs the Jiang–Su algebra tensorially, and hence is classified by its Elliott invariant.
Proof Note that
where
![]() $\mathbb Z^{d_1} \times \mathbb Z^{d_2}$
acting on
$\mathbb Z^{d_1} \times \mathbb Z^{d_2}$
acting on
![]() $X_1 \times X_2$
by
$X_1 \times X_2$
by
By the argument of Remark 5.8 of [Reference Elliott and Niu7], one has
and the statement then follows from Theorem 5.8.