Hostname: page-component-cd9895bd7-gxg78 Total loading time: 0 Render date: 2024-12-26T01:04:11.559Z Has data issue: false hasContentIssue false
  • English
  • Français

Quotient Hereditarily Indecomposable Banach Spaces

Published online by Cambridge University Press:  20 November 2018

V. Ferenczi
V. Ferenczi*
Affiliation:
Equipe d’Analyse, Université Paris 6, Tour 46-0, Boîte 186, 4, place Jussieu, 75252 PARIS Cedex 05, France email: [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

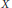A Banach space $X$ is said to be quotient hereditarily indecomposable if no infinite dimensional quotient of a subspace of 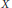$X$ is decomposable. We provide an example of a quotient hereditarily indecomposable space, namely the space 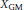${{X}_{GM}}$ constructed by W. T. Gowers and B. Maurey in 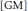$[\text{GM}]$. Then we provide an example of a reflexive hereditarily indecomposable space 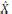$\hat{X}$ whose dual is not hereditarily indecomposable; so 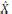$\hat{X}$ is not quotient hereditarily indecomposable. We also show that every operator on 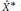${{\hat{X}}^{*}}$ is a strictly singular perturbation of an homothetic map.

Keywords

46B2047B99
Type
Research Article
Information
Canadian Journal of Mathematics , Volume 51 , Issue 3 , 01 June 1999 , pp. 566 - 584
Copyright
Copyright © Canadian Mathematical Society 1999

References

[AF] Argyros, S. and Felouzis, V., Interpolating hereditarily indecomposable Banach spaces. Preprint.Google Scholar
[F1] Ferenczi, V., Operators on subspaces of hereditarily indecomposable Banach spaces. Bull. LondonMath. Soc. 29 (1997), 338–344.Google Scholar
[F2] Ferenczi, V., Hereditarily finitely decomposable Banach spaces. Studia Math. (2) 123 (1997), 135–149.Google Scholar
[G1] Gowers, W. T., A new dichotomy for Banach spaces. Geom. Funct. Anal. (6) 6 (1996), 1083–1093.Google Scholar
[G2] Gowers, W. T., Analytic sets and games in Banach spaces. Preprint.Google Scholar
[GM] Gowers, W. T. and Maurey, B., The unconditional basic sequence problem. J. Amer. Math. Soc. 6 (1993), 851–874.Google Scholar
[LT] Lindenstrauss, J. and Tzafriri, L., Classical Banach spaces II. Springer-Verlag, New York, 1977.Google Scholar