No CrossRef data available.
Article contents
Quivers with potentials for Grassmannian cluster algebras
Published online by Cambridge University Press: 21 June 2022
Abstract
We consider a quiver with potential (QP) 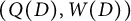 $(Q(D),W(D))$ and an iced quiver with potential (IQP)
$(Q(D),W(D))$ and an iced quiver with potential (IQP) 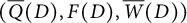 $(\overline {Q}(D), F(D), \overline {W}(D))$ associated with a Postnikov Diagram D and prove that their mutations are compatible with the geometric exchanges of D. This ensures that we may define a QP
$(\overline {Q}(D), F(D), \overline {W}(D))$ associated with a Postnikov Diagram D and prove that their mutations are compatible with the geometric exchanges of D. This ensures that we may define a QP 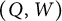 $(Q,W)$ and an IQP
$(Q,W)$ and an IQP 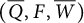 $(\overline {Q},F,\overline {W})$ for a Grassmannian cluster algebra up to mutation equivalence. It shows that
$(\overline {Q},F,\overline {W})$ for a Grassmannian cluster algebra up to mutation equivalence. It shows that 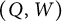 $(Q,W)$ is always rigid (thus nondegenerate) and Jacobi-finite. Moreover, in fact, we show that it is the unique nondegenerate (thus rigid) QP by using a general result of Geiß, Labardini-Fragoso, and Schröer (2016, Advances in Mathematics 290, 364–452).
$(Q,W)$ is always rigid (thus nondegenerate) and Jacobi-finite. Moreover, in fact, we show that it is the unique nondegenerate (thus rigid) QP by using a general result of Geiß, Labardini-Fragoso, and Schröer (2016, Advances in Mathematics 290, 364–452).
Then we show that, within the mutation class of the QP for a Grassmannian cluster algebra, the quivers determine the potentials up to right equivalence. As an application, we verify that the auto-equivalence group of the generalized cluster category 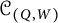 ${\mathcal {C}}_{(Q, W)}$ is isomorphic to the cluster automorphism group of the associated Grassmannian cluster algebra
${\mathcal {C}}_{(Q, W)}$ is isomorphic to the cluster automorphism group of the associated Grassmannian cluster algebra 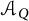 ${{\mathcal {A}}_Q}$ with trivial coefficients.
${{\mathcal {A}}_Q}$ with trivial coefficients.
MSC classification
- Type
- Article
- Information
- Copyright
- © The Author(s), 2022. Published by Cambridge University Press on behalf of The Canadian Mathematical Society
Footnotes
Wen Chang is supported by the NSF of China (Grant No. 11601295), Shaanxi Province, and Shaanxi Normal University. Jie Zhang is supported by the NSF of China (Grant Nos. 12071026 and 12122101), Beijing, and Beijing Institute of Technology.



