Hostname: page-component-586b7cd67f-t7czq Total loading time: 0 Render date: 2024-11-26T03:19:08.344Z Has data issue: false hasContentIssue false
  • English
  • Français

Quaternions and Some Global Properties of Hyperbolic 5-Manifolds

Published online by Cambridge University Press:  20 November 2018

Ruth Kellerhals
Ruth Kellerhals*
Affiliation:
University of Fribourg, Department for Mathematics, CH–1700 Fribourg, Switzerland e-mail: [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

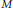We provide an explicit thick and thin decomposition for oriented hyperbolic manifolds $M$ of dimension 5. The result implies improved universal lower bounds for the volume 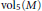$\text{vo}{{\text{l}}_{\text{5}}}\left( M \right)$ and, for 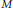$M$ compact, new estimates relating the injectivity radius and the diameter of 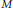$M$ with 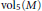$\text{vo}{{\text{l}}_{\text{5}}}\left( M \right)$. The quantification of the thin part is based upon the identification of the isometry group of the universal space by the matrix group 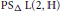$\text{P}{{\text{S}}_{\Delta }}\text{L}\left( 2,\,\mathbb{H} \right)$ of quaternionic 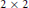$2\,\times \,2$-matrices with Dieudonné determinant 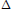$\Delta$ equal to 1 and isolation properties of 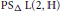$\text{P}{{\text{S}}_{\Delta }}\text{L}\left( 2,\,\mathbb{H} \right)$.

Keywords

53C2253C2557N1657S3051N3020G2022E40
Type
Research Article
Information
Canadian Journal of Mathematics , Volume 55 , Issue 5 , 01 October 2003 , pp. 1080 - 1099
Copyright
Copyright © Canadian Mathematical Society 2003

References

[Al] Ahlfors, L. V., Möbius transformations and Clifford numbers. In: Differential geometry and complex analysis. A volume dedicated to the memory of Harry Ernest Rauch. Eds. Chavel, I. and Farkas, H. M.. Springer-Verlag, Berlin, 1985.Google Scholar
[As] Aslaksen, H., Quaternionic determinants. Math. Intelligencer, 18(1996), 57–65.Google Scholar
[BGS] Ballmann, W., Gromov, M. and Schroeder, V., Manifolds of nonpositive curvature. Birkhäuser, 1985.Google Scholar
[Be] Beardon, A. F., The geometry of discrete groups. Springer-Verlag, 1983.Google Scholar
[Bu1] Buser, P., On Cheeger's inequality, λ 1 ≤ h2/4. In: Geometry of the Laplace operator, 29–77, Proc. Sympos. Pure Math. XXXVI, Amer. Math. Soc., Providence, R.I., 1980.Google Scholar
[Bu2] Buser, P., Geometry and spectra of compact Riemann surfaces. Birkhäuser, 1992.Google Scholar
[CGM] Cao, C., Gehring, F. W. and Martin, G. J., Lattice constants and a lemma of Zagier. In: Lipa's legacy. Proceedings of the 1st Bers Colloquium. Eds. Dodziuk, J. et al. Contemp. Math. 211(1997), 107–120.Google Scholar
[CW] Cao, C. and Waterman, P. L., Conjugacy invariants of Möbius groups. In: Quasiconformal Mappings and Analysis, A collection of papers honoring F.W. Gehring. Eds. Duren, Peter, et al., Springer-Verlag, New York, 1998.Google Scholar
[C1] Coxeter, H. S. M., Quaternions and reflections. Amer. Math. Monthly 53(1946), 136–146.Google Scholar
[C2] Coxeter, H. S. M., Regular complex polytopes. Cambridge University Press, 1974.Google Scholar
[D] Dieudonné, J., Les déterminants sur un corps non-commutatif. Bull. Soc. Math. France 71(1943), 27–45.Google Scholar
[HK] Heintze, E. and Karcher, H., A general comparison theorem with applications to volume estimates for submanifolds. Ann. Sci. École Norm. Sup. 11(1978), 451–470.Google Scholar
[H] Hellegouarch, Y., Quaternionic homographies: application to Ford hyperspheres. C. R. Math. Rep. Acad. Sci. Canada 11(1989), 165–170.Google Scholar
[J] Jørgensen, T., On discrete groups of Möbius transformations. Amer. J. Math. 98(1976), 739–749.Google Scholar
[K1] Kellerhals, R., Regular simplices and lower volume bounds for hyperbolic n-manifolds. Ann. Global Anal. Geom. 13(1995), 377–392.Google Scholar
[K2] Kellerhals, R., Volumes of cusped hyperbolic manifolds. Topology 37(1998) 719–734.Google Scholar
[K3] Kellerhals, R., Collars i. PSL(2;H). Ann. Acad. Sci. Fenn.Math. 26(2001), 51–72.Google Scholar
[M] Meyerhoff, R., A lower bound for the volume of hyperbolic 3-manifolds. Canad. J. Math. 39(1987), 1038–1056.Google Scholar
[Po] Porteous, I. R., Topological geometry. Cambridge University Press, 1981.Google Scholar
[Pr] Przeworski, A., Cones embedded in hyperbolic manifolds. J. Differential Geom. 58(2001), 219–232.Google Scholar
[R1] Ratcliffe, J. G., Foundations of hyperbolic manifolds. Springer-Verlag, 1994.Google Scholar
[R2] Ratcliffe, J. G., Hyperbolic manifolds. In: Handbook of geometric topology. Eds., Daverman, R. J. and Sher, R. B., Elsevier, 2001.Google Scholar
[Re] Reznikov, A., The volume and the injectivity radius of a hyperbolic manifold. Topology 34(1995), 477–479.Google Scholar
[T] Thurston, W. P., Three-dimensional geometry and topology, vol. 1. Princeton University Press, 1997.Google Scholar
[Wat] Waterman, P. L., Möbius transformations in several dimensions. Adv. in Math. 101(1993), 87–113.Google Scholar
[Wil] Wilker, J. B., The quaternion formalism for Möbius groups in four and fewer dimensions. Linear Algebra Appl. 190(1993), 99–136.Google Scholar