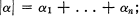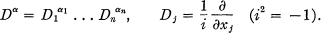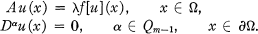Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Adams, R. A.
1966.
A Quasi-Linear Elliptic Boundary Value Problem.
Canadian Journal of Mathematics,
Vol. 18,
Issue. ,
p.
1105.
Gordinskii, L. D.
1972.
On a boundary-value problem for a system of elliptic differential equations.
Ukrainian Mathematical Journal,
Vol. 24,
Issue. 5,
p.
555.
de Figueiredo, Djairo Guedes
1975.
Djairo G. de Figueiredo - Selected Papers.
p.
43.
de Figueiredo, Djairo Guedes
1975.
Partial Differential Equations and Related Topics.
Vol. 446,
Issue. ,
p.
144.