Hostname: page-component-cd9895bd7-gvvz8 Total loading time: 0 Render date: 2024-12-26T12:58:41.208Z Has data issue: false hasContentIssue false
  • English
  • Français

Quasiconvex Sets

Published online by Cambridge University Press:  20 November 2018

J. W. Green  and
W. Gustin
J. W. Green
Affiliation:
U.C.L.A. and Indiana University
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

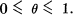Introduction. Let I be the closed real number interval: Any subset Δ of I containing at least one number interior to I, will be called a quasiconvexity generating set. To each quasiconvexity generating set Δ we associate as follows a generalized notion of convexity, here called quasiconvexity or Δ convexity. Two numbers α and β, one of which belongs to Δ, the other being determined by the relation a α + β = 1, are called complementary ratios of Δ. A set Q in a real vector space is said to be A convex if for every pair of complementary ratios α and β in Δ and every pair of points a and b lying in Q the point αa +β b also lies in Q.

Type
Research Article
Information
Canadian Journal of Mathematics , Volume 2 , 1950 , pp. 489 - 507
Copyright
Copyright © Canadian Mathematical Society 1950

References

[1] Alexiewicz, A. and Orlicz, W., Remarque sur l-equation fonctionelle, f(x + y) = f(x) + f(y). Fund. Math., vol. 33 (1945), 314–315.Google Scholar
[2] Banach, S., Sur Véquation fonctionelle f(x + y) = f(x) + f(y), Fund. Math., vol. 1 (1920), 123–124.Google Scholar
[3] Beckenbach, E. F., Convex Functions, Bull. Amer. Math. Soc, vol. 54 (1948), 439–460.Google Scholar
[4] Beckenbach, E. F. and Bing, R. H., On generalized convex functions, Trans. Amer. Math. Soc, vol. 58 (1945), 220–230.Google Scholar
[5] Bernstein, F., Über das Gausssche Fehlergesetz, Math. Ann., vol. 64 (1907), 417–448.Google Scholar
[6] Bernstien, F. and Doetsch, G., Zur Théorie der konvexen Funktionen, Math. Ann., vol. 76 (1915), 514–526.Google Scholar
[7] Blumberg, H., Convex functions, Trans. Amer. Math. Soc, vol. 20 (1919), 40–44.Google Scholar
[8] Burstin, C., Die Spaltung des Kontinuum in c in L Sinne nichtmessbare Mengen, Sitzber. Akad. Wiss. Vienna, Math-nat. KL, Abt, lia, vol. 125 (1916), 209–317.Google Scholar
[9] Cauchy, A. L., Cours d'analyse de l' École Royale Polytechnique, part 1, Analyse algébrique (Paris, 1821).Google Scholar
[10] Darboux, G., Sur la composition des forces en statique, Bull. Sci. Math., vol. 9 (1875), 281–288.Google Scholar
[11] Darboux, G., Sur la théoréme fondamental de la géométrie projective, Math. Ann., vol. 17 (1880), 55–61.Google Scholar
[12] Fréchet, M., Pri la funkcia ekvacio f(x + y)=f(x) + f(y), Ens. Math., vol. 15 (1913),390–393.Google Scholar
[13] Hamel, G., Über die Zusammensetzung von Vektoren, Zeit. Math. Phys., vol. 49, 362–371.Google Scholar
[14] Hamel, G., Eine Basis aller Zahlen und die unstetigen Lösungen der Funktionalgleichung: f(x) + f(y) = f(x + y), Math. Ann., vol. 60 (1905), 459–462.Google Scholar
[15] Jensen, J. L. W. V., Om konvexe Funktioner og Uligheder mellem Middelvaerdier, Nyt. Tidsskrift for Mathematik, vol. 16B (1905), 49–69.Google Scholar
[16] Jensen, J. L. W. V., Sur les fonctions convexes et les inégalités entre les valeurs moyennes, Acta Math., vol. 30 (1906), 175–193.Google Scholar
[17] Jones, F. B., Connected and disconnected plane sets and the functional equation f(x) + f(y) = f(x + y), Bull. Am. Math. Soc, vol. 48 (1942), 115–120.Google Scholar
[18] Jones, F. B., Measure and other properties of a Hamel basis, Bull. Amer. Math. Soc, vol. 48 (1942), 472–481.Google Scholar
[19] Kac, M., Une remarque sur les équations fonctionelles, Comm. Math. Helv., vol. 9 (1936/37), 170–171.Google Scholar
[20] Kestelman, H., On the functional equation f(x + y) = f(x) + f(y), Fund. Math., vol. 34 (1947), 144–147.Google Scholar
[21] Lebesgue, H., Sur les transformations ponctuelles, transformant les plans en plans, qu' onpeut définir par des procédés analytiques, Atti R. Ac Se Torino, vol. 42 (1907).Google Scholar
[22] Ostrowski, A., Über die Funktionalgleichung der Exponentialfunktion und verwandte Funktionalgleichung, Jber. Deut. Math. Ver., vol. 38 (1929), 54–62.Google Scholar
[23] Ostrowski, A., Zur Théorie der konvexen Funktionen, Comm. Math. Helv., vol. 1 (1929), 157–159.Google Scholar
[24] Ramaswami, V., On the continuity of convex functions, J. Benares Hindu Univ., vol. 7, part 1 (1943), 180–181.Google Scholar
[25] Ruziewicz, S., Une application de l'équation fonctionelle f(x + y) = f(x) + f(y) à la décomposition de la droite en ensembles superposables, non mesurables, Fund. Math., vol. 5 (1924), 92–95.Google Scholar
[26] Ruziewicz, S., Contribution à l'étude des ensembles des distances de points, Fund. Math., vol. 7 (1925), 141–143.Google Scholar
[27] Schimmack, R., Über die axiomatische Begründung der Vektoraddition, Gö tt. Nach. (1903), 317–325.Google Scholar
[28] Schimmack, R., Axiomatische Untersuchungen Über die Vektor addition, Nova Acta Ac Leop., vol. 90, 5–104.Google Scholar
[29] Schur, F., Über die Zusammenhang von Vektoren, Zeit. Math. Phys., vol. 49, 352–361.Google Scholar
[30] Sierpinski, W., Sur la question de la mesurabilité de la base de M. Hamel, Fund. Math., vol. 1 (1920), 105–111.Google Scholar
[31] Sierpinski, W., Sur Véquation fonctionelle f(x ' y) = f(x) + f(y), Fund. Math., vol. 1 (1920), 116–122.Google Scholar
[32] Sierpinski, W., Sur les fonctions convexes mesurables, Fund. Math., vol. 1 (1920), 125–129.Google Scholar
[33] Sierpinski, W., Sur Vensemble de distance entre les points d'un ensemble. Fund. Math., vol. 7 (1925), 144–148.Google Scholar
[34] Sierpinski, W., Sur une propriété des fonctions de M.Hamel, Fund. Math., vol. 5 (1924), 334–336.Google Scholar
[35] Steinhaus, H., Sur les distances des points des ensembles de mesure positive, Fund. Math. vol. 1 (1920), 93–104.Google Scholar