Hostname: page-component-cd9895bd7-8ctnn Total loading time: 0 Render date: 2024-12-24T00:56:52.638Z Has data issue: false hasContentIssue false
  • English
  • Français

Quantum Families of Invertible Maps and Related Problems

Published online by Cambridge University Press:  20 November 2018

Adam Skalski  and
Piotr Sołtan
Adam Skalski
Affiliation:
Institute of Mathematics of the Polish Academy of Sciences, ul. Śniadeckich 8, 00-956 Warszawa, Poland and Faculty of Mathematics, Informatics and Mechanics, University of Warsaw, ul. Banacha 2, 02-097 Warsaw, Poland e-mail: [email protected]
Piotr Sołtan
Affiliation:
Department of Mathematical Methods in Physics, Faculty of Physics, University of Warsaw, Poland e-mail: [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

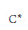The notion of families of quantum invertible maps (${{C}^{*}}$-algebra homomorphisms satisfying Podleś condition) is employed to strengthen and reinterpret several results concerning universal quantum groups acting on finite quantum spaces. In particular, Wang's quantum automorphism groups are shown to be universal with respect to quantum families of invertible maps. Further, the construction of the Hopf image of Banica and Bichon is phrased in purely analytic language and employed to define the quantum subgroup generated by a family of quantum subgroups or, more generally, a family of quantum invertible maps.

Keywords

46L8946L65quantum families of invertible maps Hopf imageuniversal quantum group
Type
Research Article
Information
Canadian Journal of Mathematics , Volume 68 , Issue 3 , 01 June 2016 , pp. 698 - 720
Copyright
Copyright © Canadian Mathematical Society 2016

References

[Ba1] Banica, T., Symmetries of a generic coaction. Math. Ann. 314 (1999), no.7, 763–780. http://dx.doi.org/10.1007/s002080050315 Google Scholar
[Ba2] Banica, T., Quantum permutations, Hadamard matrices, and the search for matrix models. In:Operator algebras and quantum groups, Banach Center Publ., , Polish Acad. Sci. Inst. Math. Warsaw, 2012, pp. 11℃42 http://dx.doi.org/10.4064/bc98-0-1 Google Scholar
[BaB]Banica, T. and Bichon, J., Hopf images and inner faithful representations. Glasg. Math. J. 52(2010), no. 3, 677–703. http://dx.doi.org/10.1017/S0017089510000510 Google Scholar
[BBC] Banica, T., Bichon, J., and Collins, B., Quantum permutation groups: a survey. In: Noncommutative harmonic analysis with applications to probability, Banach Center Publ. 78,Polish Acad. Sci. Inst. Math.,Warsaw, 2007, pp.13–34. http://dx.doi.org/10.4064/bc78-0-1 Google Scholar
[BFS] Banica, T., Franz, U., and Skalski, A.,Idempotent states and the inner linearity property. Bull. Polish. Acad. Sci. Math 60 (2012), no. 2, 123℃132 http://dx.doi.org/10.4064/ba60-2-3 Google Scholar
[Boc] Boca, F. P., Ergodic actions of compact matrix pseudogroups on C*℃algebras. In: Recent Advances in Operator algebras(Orle,1992), Astérisque 232(1995),93–109.Google Scholar
[Bra] Brannan, M., Reduced operator algebras of trace-preserving quantum automorphism groups. Doc. Math. 18(2013), 1349–1402.Google Scholar
[BCV] Brannan, M., Collins, B., and Vergnioux, R.,The Connes embedding property for quantum group von Neumann algebras. Trans. Amer. Math. Soc., to appear. arxiv:1412.7788Google Scholar
[Cur] Curran, S., A characterization of freeness by invariance under quantum spreading. J. Reine Angew. Math. 659(2011), 43–65. http://dx.doi.org/10.1515/CRELLE.2011.066 Google Scholar
[DKSS] Daws, M., Kasprzak, P., Skalski, A., and Sołtan, P. M., Closed quantum subgroups of locally compact quantum groups. Adv. Math. 231(2012), 3473–3501. http://dx.doi.org/10.1016/j.aim.2012.09.002 Google Scholar
[NeY] Neshveyev, S. and Yamashita, M., Categorical duality for Yetter-Drinfeld algebras. Doc. Math. 19(2014), 1105–1139.Google Scholar
[Poi] Podleś, P., Przestrzenie kwantowe i ich grupy symetrii (Quantum spaces and their symmetry groups) (Polish). PhD Thesis, Department of Mathematical Methods in Physics, Faculty of Physics, Warsaw University, 1989.Google Scholar
[P02] Podleś, P. , Symmetries of quantum spaces. Subgroups and quotient spaces of quantum SU(2) and SO(3) groups. Commun. Math. Phys. 170(1995), 1–20.http://dx.doi.Org/10.1007/BF02099436 Google Scholar
[So1] Soltan, P. M., Quantum families of maps and quantum semigroups on finite quantum spaces. J. Geom. Phys. 59(2009), 354–368.http://dx.doi.Org/10.1 01 6/j.geomphys.2008.11.007 Google Scholar
[S02] Soltan, P. M., On quantum semigroup actions on finite quantum spaces. Infin. Dimens. Anal. Quantum Probab. Relat. Top. 12(2009), 503–509.http://dx.doi.org/10.1142/S0219025709003768 Google Scholar
[S03] Soltan, P. M., Examples of non-compact quantum group actions. J. Math. Anal. Appl. 372(2010), no. 1, 224–236.http://dx.doi.Org/10.106/j.jmaa.2O10.06.045 Google Scholar
[VDW]Daele, A. Van and Wang, S., Universal quantum group. Internat. J. Math. 7(1996), 255–263.http://dx.doi.Org/10.1142/S0129167X96000153 Google Scholar
[Voi] Voigt, C., On the structure of quantum automorphism groups. J. Reine Angew. Math., to appear.arxiv:1411.1939Google Scholar
[Wa] Wang, S., Lp ℃improving convolution operators on finite quantum groups. Indiana Univ. Math. J.,to appear. arxiv:1412.2085Google Scholar
[Wan] Wang, S., Quantum symmetry groups of finite spaces. Commun. Math. Phys. 195(y), no. 1, 195–211. http://dx.doi.org/10.1007/s002200050385 Google Scholar
[Was] S. Wassermann, Exact C*-algebras and related topics. Seoul National University, Research Institute of Mathematics, Global Analysis Research Center, 1994.Google Scholar
[Woi] Woronowicz, S. L., Pseudogroups, pseudospaces andPontryagin duality. In: Mathematical problems in theoretical physics (Proc. Internat. Conf. Math. Phys., Lausanne 1979), Lecture Notes in Physics, 116, Springer, Berlin-New York, 1980, pp. 407–412.Google Scholar
[W02] Woronowicz, S. L., A remark on compact quantum matrix groups. Lett. Math. Phys. 21(1991), no. 1, 35–39.http://dx.doi.Org/10.1007/BF00414633 Google Scholar
[W03] Woronowicz, S. L., Compact quantum groups. In: Symétries quantiques, Les Houches, Session LXIV 1995, North-Holland, Amsterdam, 1998, pp. 845–884.Google Scholar
[W04] Woronowicz, S. L., C*-algebras generated by unbounded elements. Rev. Math. Phys. 7(1995), 481–521.http://dx.doi.org/10.1142/S0129055X95000207 Google Scholar