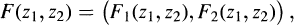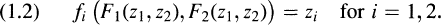Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Krattenthaler, Christian
and
Schlosser, Michael
1999.
A new multidimensional matrix inverse with applications to multiple q-series.
Discrete Mathematics,
Vol. 204,
Issue. 1-3,
p.
249.
Ismail, Mourad
and
Rahman, Mizan
2011.
Connection relations and expansions.
Pacific Journal of Mathematics,
Vol. 252,
Issue. 2,
p.
427.


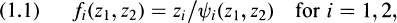
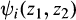 is an fps with
is an fps with  for i = 1,2. Then there exists a unique pair of fps
for i = 1,2. Then there exists a unique pair of fps