No CrossRef data available.
Article contents
Purity And Copurity in Systems of Linear Transformations
Published online by Cambridge University Press: 20 November 2018
Extract
Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.
Consider a system of N linear transformations A1, … , AN: V → W, where F and IF are complex vector spaces. Denote it for short by (F, W). A pair of subspaces X ⊂ V, Y ⊂ W such that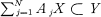 
determines a subsystem (X, Y) and a quotient system (V/X, W/Y) (with the induced transformations). The subsystem (X, Y) is of finite codimension in (V, W) if and only if V/X and W / Y are finite-dimensional. It is a direct summand of (V, W) in case there exist supplementary subspaces P of X in F and Q of F in IF such that (P, Q) is a subsystem.
- Type
- Research Article
- Information
- Copyright
- Copyright © Canadian Mathematical Society 1976
References
1.
Aronszajn, N., Quadratic forms on vector spaces, Proc. Intern. Symposium on Linear Spaces 1960 (Jerusalem, 1961).Google Scholar
2.
Aronszajn, N. and Fixman, U., Algebraic spectral problems,
Studia Math.
30 (1968), 273–338.Google Scholar
3.
Fixman, U., On algebraic equivalence between pairs of linear transformations,
Trans. Amer. Math. Soc.
113 (1964), 424–453.Google Scholar
4.
Fixman, U. and Zorzitto, F., Direct summands of systems of continuous linear transformations, Queen's University Math, preprint, 1975.Google Scholar
5.
Fixman, U. and Zorzitto, F., A purity criterion for pairs of linear transformations,
Can. J. Math.
26 (1974), 734–745.Google Scholar
6.
Robertson, A. P. and Robertson, W. J., Topological vector spaces (Cambridge Univ. Press, Cambridge, 1964).Google Scholar
7.
Zorzitto, F., Topological decompositions in systems of linear transformations, Ph.D. thesis, Queen's University, Kingston, Ontario, 1972.Google Scholar
You have
Access