Hostname: page-component-cd9895bd7-gxg78 Total loading time: 0 Render date: 2024-12-25T02:27:47.513Z Has data issue: false hasContentIssue false
  • English
  • Français

Pure Infiniteness of the Crossed Product of an AH-Algebra by an Endomorphism

Published online by Cambridge University Press:  20 November 2018

Klaus Thomsen
Klaus Thomsen*
Affiliation:
Institut for matematiske fag, Ny Munkegade, 8000 Aarhus C, Denmark e-mail: [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

It is shown that simplicity of the crossed product of a unital 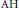$\text{AH}$-algebra with slow dimension growth by an endomorphism implies that the algebra is also purely infinite, provided only that the endomorphism leaves no trace state invariant and takes the unit to a full projection.

Keywords

46-xxpurely infinite C*-algebrascrossed products
Type
Research Article
Information
Canadian Journal of Mathematics , Volume 64 , Issue 3 , 01 June 2012 , pp. 705 - 720
Copyright
Copyright © Canadian Mathematical Society 2012

References

[An] Anantharaman-Delaroche, C., Purely infinite C*-algebras arising from dynamical systems. Bull. Soc. Math. France 125(1997), no. 2, 199–225.Google Scholar
[BKR] Boyd, S., Keswari, N., and Raeburn, I., Faithful representations of crossed products by endomorphisms. Proc. Amer. Math. Soc. 118(1993), no. 2, 427–436. http://dx.doi.org/10.1090/S0002-9939-1993-1126190-X Google Scholar
[CT] Carlsen, T. M. and Thomsen, K., The structure of the C*-algebra of a locally injective surjection. Ergodic Theory and Dynamical Systems, to appear, available on CJO 2011. http://dx.doi.org/10.1017/S0143385711000216 http://dx.doi.org/10.1007/s00220-010-1168-7 Google Scholar
[De] Deaconu, V., Groupoids associated with endomorphisms. Trans. Amer. Math. Soc. 347(1995), no. 5, 1779–1786. http://dx.doi.org/10.2307/2154972 Google Scholar
[DR] Dykema, K. and M. Rørdam, Purely infinite, simple C*-algebras arising from free product constructions. Canad. J. Math. 50(1998), no. 2, 323–341. http://dx.doi.org/10.4153/CJM-1998-017-x Google Scholar
[KR] Kirchberg, E. and M. Rørdam, Non-simple purely infinite C*-algebras. Amer. J. Math. 122(2000), no. 3, 637–666. http://dx.doi.org/10.1353/ajm.2000.0021 Google Scholar
[OP1] Olesen, D. and Pedersen, G. K., Applications of the Connes spectrum to C*-dynamical systems. J. Funct. Anal. 30(1978), no. 2, 179–197. http://dx.doi.org/10.1016/0022-1236(78)90069-1 Google Scholar
[OP2] Olesen, D. and Pedersen, G. K., Applications of the Connes spectrum to C*-dynamical systems. III. J. Funct. Anal. 45(1982), no. 3, 357–390. http://dx.doi.org/10.1016/0022-1236(82)90011-8 Google Scholar
[Pe] Pedersen, G. K., C*-algebras and their automorphism groups. London Mathematical Society Monographs, 14, Academic Press, London-New York, 1979.Google Scholar
[PS] Putnam, I. and Spielberg, J., The structure of C*-algebras associated with hyperbolic dynamical systems. J. Func. Anal. 163(1999), no. 2, 279–299. http://dx.doi.org/10.1006/jfan.1998.3379 Google Scholar
[R1] Rørdam, M., Classification of certain infinite simple C*-algebras. J. Funct. Anal. 131(1995), no. 2, 415–458. http://dx.doi.org/10.1006/jfan.1995.1095 Google Scholar
[R2] Rørdam, M., Classification of certain infinite simple C*-algebras. III. In: Operator algebras and their applications (Waterloo, ON, 1994/1995), Fields Inst. Commun., 13, American Mathematical Society, 1997.Google Scholar
[St] Stacey, P. J., Crossed products of C*-algebras by endomorphisms. J. Austral. Math. Soc. 54(1993), no. 2, 204–212. http://dx.doi.org/10.1017/S1446788700037113 Google Scholar
[Th1] Thomsen, K., Semi-étale groupoids and applications. Ann. Inst. Fourier 60(2010), no. 3, 759–800. http://dx.doi.org/10.5802/aif.2539 Google Scholar
[Th2] Thomsen, K., Inductive limits of interval algebras: the simple case. In: Quantum and non-commutative analysis (Kyoto, 1992), Math. Phys. Stud., 16, Kluwer Acad. Publ. Dordrecht, 1993, 399–404.Google Scholar
[T] Toms, A. S., Comparison theory and smooth minimal C*-dynamics. Comm. Math. Phys. 289(2009), no. 2, 401–433. http://dx.doi.org/10.1007/s00220-008-0665-4 Google Scholar
[W] Winter, W., Nuclear dimension and Z-stability of perfect C*-algebras. arxiv:1006.2731v1Google Scholar